Trigonométrie et vecteurs
Pourquoi deux thèmes pour un seul cours ?
La trigonométrie est l'étude des angles et des distances dans un triangle. Si ça semble être un champ bien réduit des mathématiques, c'est en fait la base d'une bonne partie de la géométrie. En effet, on peut schématiser beaucoup de situations avec un triangle rectangle : on peut trouver des relations entre ses distances (Pythagore, Thalès), entre ses angles (angles supplémentaires, opposés, alternés...), et entre les distances et les angles (SOH CAH TOA).
Les vecteurs sont des quantités géométriques ayant une norme (longueur) et une direction (angle).
Il suffit donc de trouver les points communs : les vecteurs impliquent des distances et des angles, et la trigonométrie justement s'occupe de distances et d'angles. Dans ce cours, nous allons donc étudier les vecteurs et utiliser la trigonométrie pour les interpréter. Ce faisant, nous atteindrons les objectifs listés ci-dessous.
Objectifs pédagogiques
Les angles et le cercle trigonométrique
- Utiliser le cercle trigonométrique pour placer les images de réels x, et trouver graphiquement les images de ces réels modifiés de quantités en radians (fractions de pi); convertir des angles de degrés à radians, et inversement.
- Revoir les différentes relations entre les angles : complémentaires, supplémentaires, opposés.
Propriétés et utilisation des fonctions trigonométriques
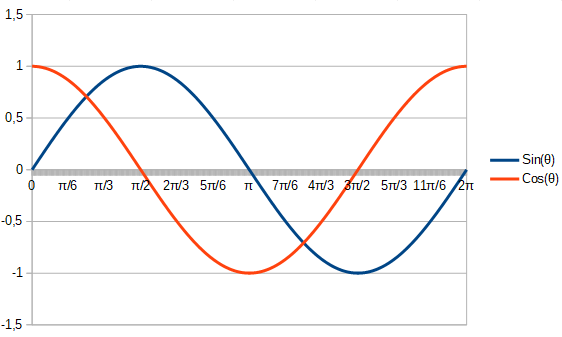
- Déterminer graphiquement et à l'aide d'une calculatrice le sinus ou le cosinus d'un angle; apprendre certaines propriétés des fonctions trigonométriques (bornes, somme des carrés...).
- Représenter une fonction trigonométrique sur un graphique et faire le lien entre déplacement angulaire et déplacement linéaire; comparer les fonctions sinus et cosinus.
- Utiliser les fonctions trigonométriques pour calculer des distances et des angles dans un triangle rectangle.
Définition et utilisation des vecteurs
- Représenter et déterminer graphiquement les coordonnées d'un vecteur.
- Effectuer des calculs sur des vecteurs: addition, soustraction, et multiplication scalaire.
- Utiliser les fonction trigonométriques pour analyser des vecteurs; application des vecteurs et de la trigonométrie en Physique.
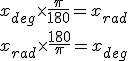
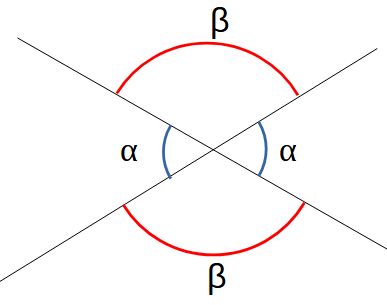 Deux lignes droites qui se croisent forment deux paires d'angles opposés. Chaque angle d'une paire est égal à l'autre.
Deux lignes droites qui se croisent forment deux paires d'angles opposés. Chaque angle d'une paire est égal à l'autre.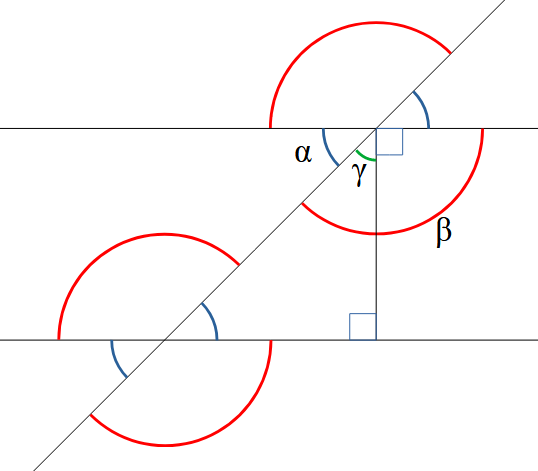 On déduit de cette première propriété une seconde : deux lignes parallèles coupées par une troisième forment les mêmes angles. Si on dessine un segment perpendiculaire aux deux lignes parallèles, on forme un triangle rectangle.
On déduit de cette première propriété une seconde : deux lignes parallèles coupées par une troisième forment les mêmes angles. Si on dessine un segment perpendiculaire aux deux lignes parallèles, on forme un triangle rectangle.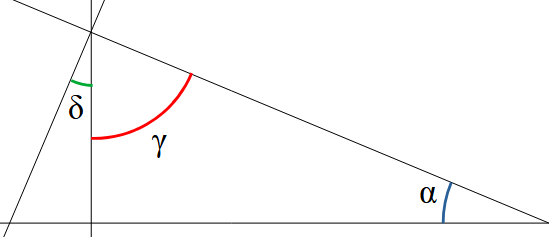 Forts de ces propriétés, on peut facilement trouver des angles dans des situations relativement complexes. Par exemple, dans l'exemple ci-contre, on connaît l'angle α et on souhaite connaître l'angle δ. On note que les angles γ et δ sont complémentaires. Comme on sait que la somme de α et γ est égale à 90°, on en déduit que δ et α sont égaux.
Forts de ces propriétés, on peut facilement trouver des angles dans des situations relativement complexes. Par exemple, dans l'exemple ci-contre, on connaît l'angle α et on souhaite connaître l'angle δ. On note que les angles γ et δ sont complémentaires. Comme on sait que la somme de α et γ est égale à 90°, on en déduit que δ et α sont égaux.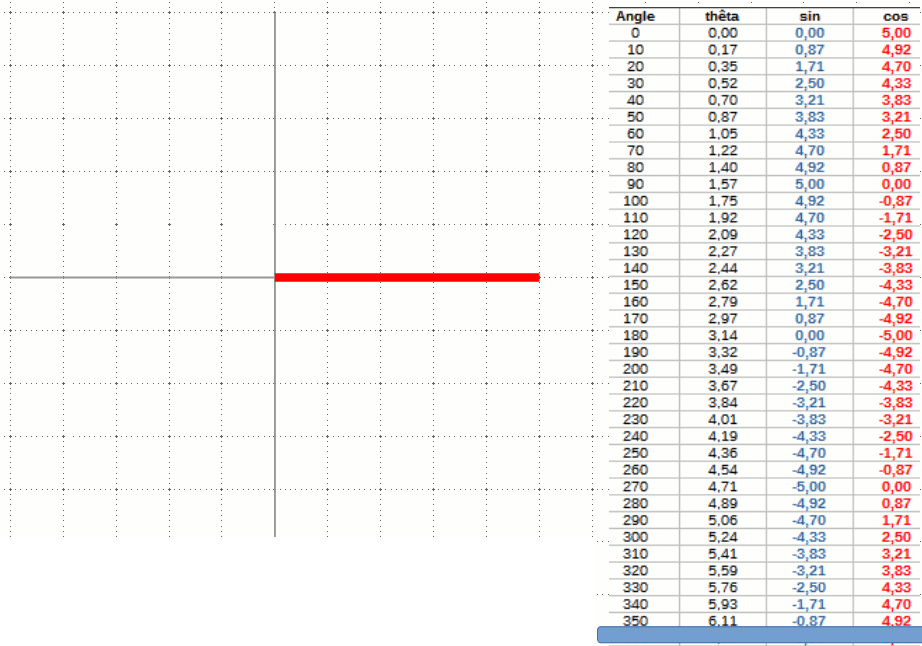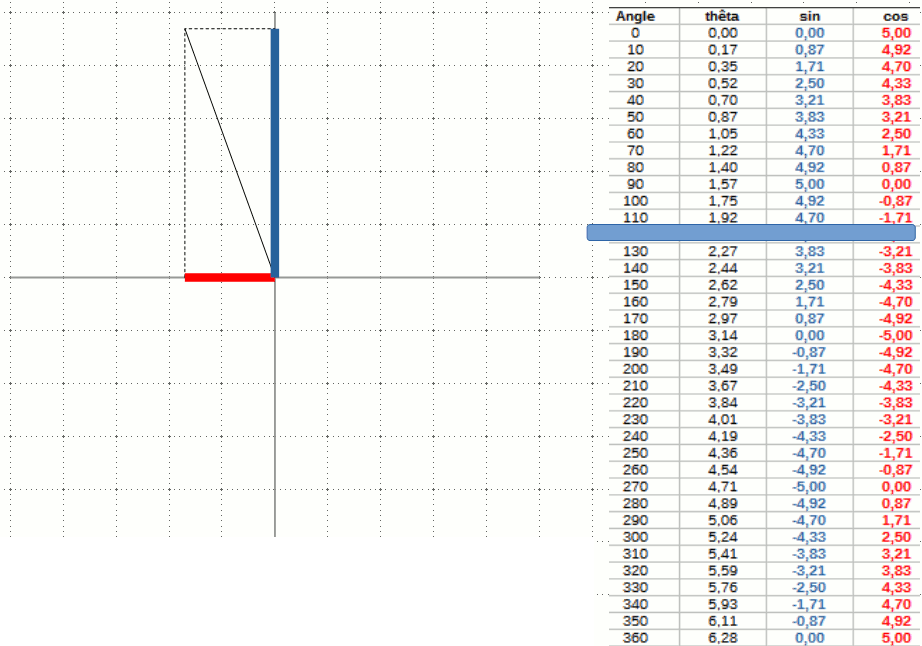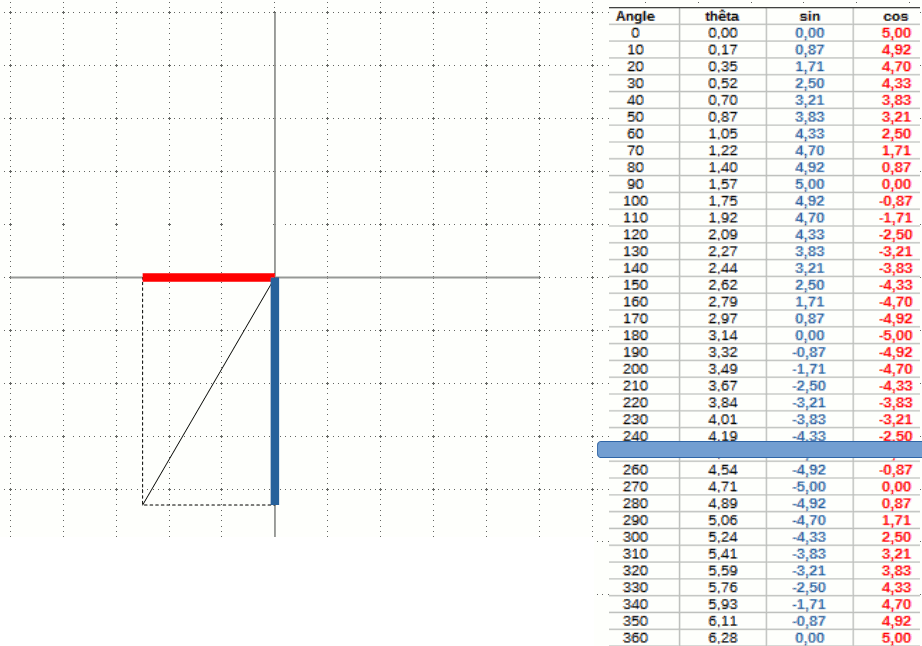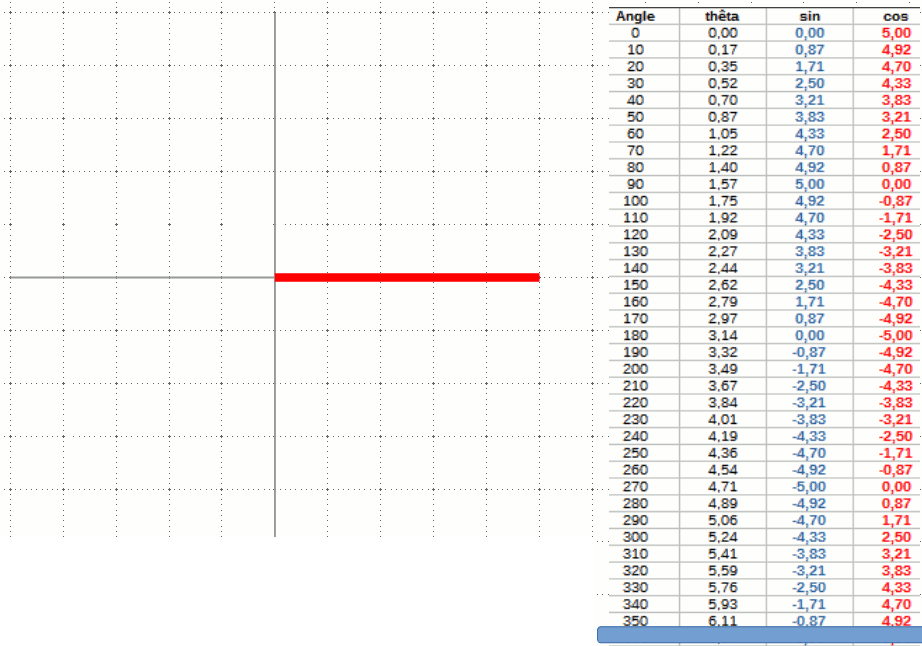
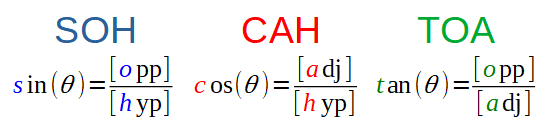
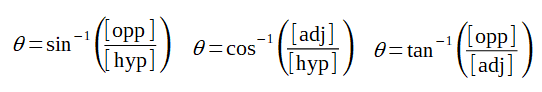
 Les propriétés des fonctions trigonométriques intéressantes sont nombreuses. Rien que pour les identités, il existe
Les propriétés des fonctions trigonométriques intéressantes sont nombreuses. Rien que pour les identités, il existe 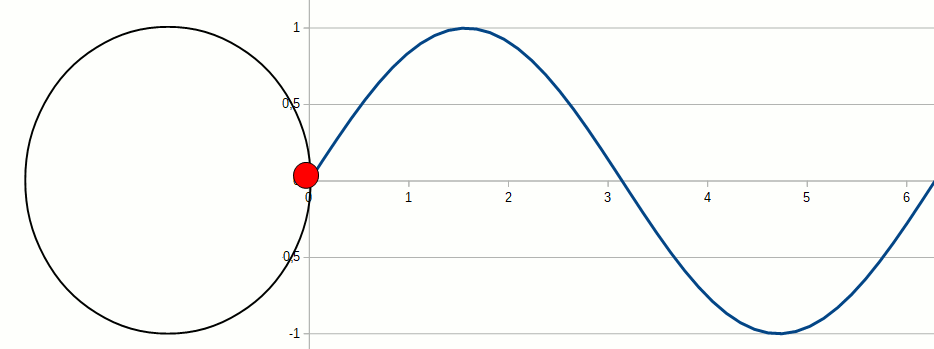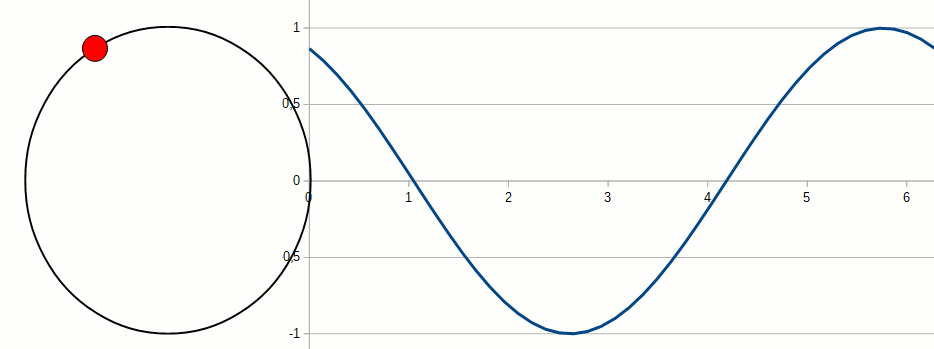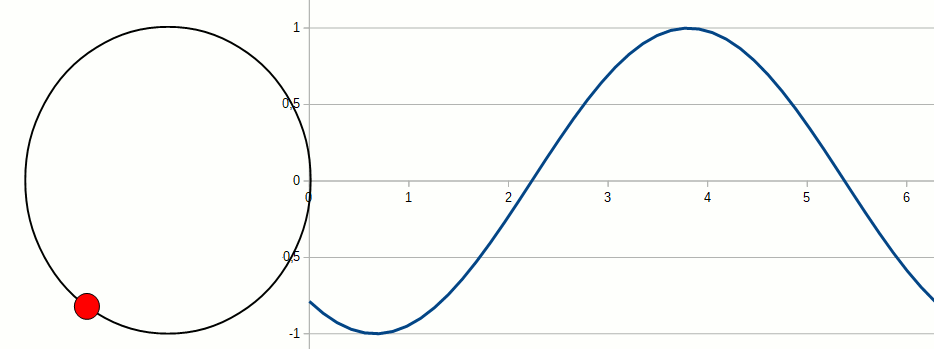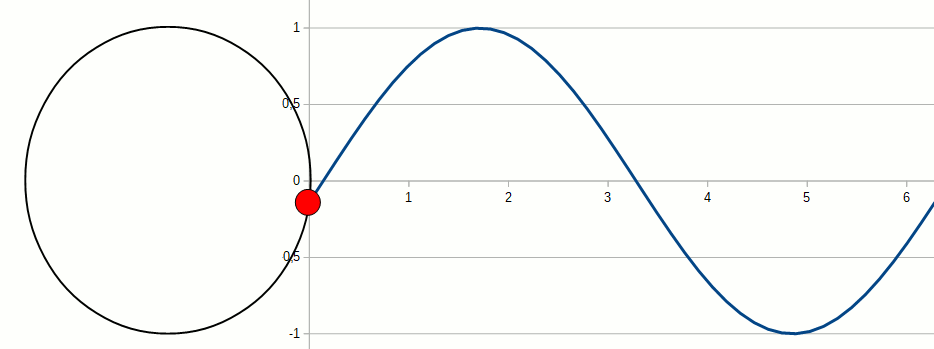
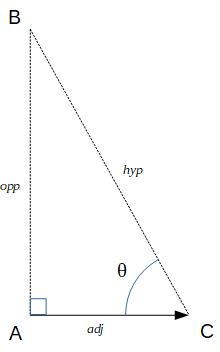 On a vu que les fonctions trigonométriques peuvent être utilisées pour décrire une onde ou un mouvement rotationnel. Dans le cadre de ce cours, nous ne les utiliserons que pour la géométrie et leur application dans le calcul de distances dans un triangle rectangle. Pour rappel, le côté le plus long d'un triangle rectangle s'appelle l'hypoténuse.
On a vu que les fonctions trigonométriques peuvent être utilisées pour décrire une onde ou un mouvement rotationnel. Dans le cadre de ce cours, nous ne les utiliserons que pour la géométrie et leur application dans le calcul de distances dans un triangle rectangle. Pour rappel, le côté le plus long d'un triangle rectangle s'appelle l'hypoténuse.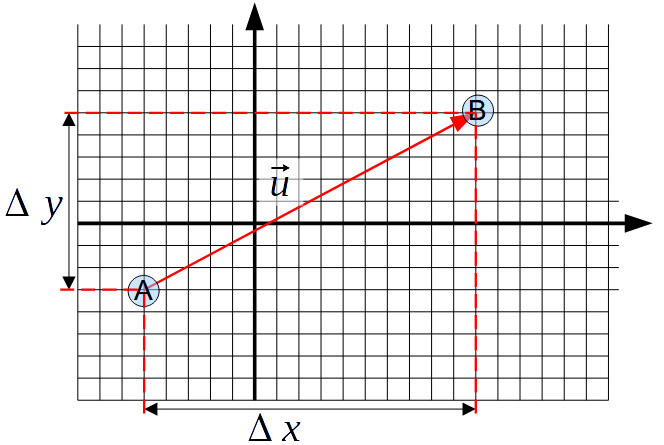 Comme on l'a déjà dit, un vecteur représente deux quantités : une norme ou longueur et une direction. Certains ouvrages sont plus précis et descriptifs et parlent de trois quantités: une norme, une direction et un sens. Dans ce cours, nous considérerons que la direction inclus le sens.
Comme on l'a déjà dit, un vecteur représente deux quantités : une norme ou longueur et une direction. Certains ouvrages sont plus précis et descriptifs et parlent de trois quantités: une norme, une direction et un sens. Dans ce cours, nous considérerons que la direction inclus le sens.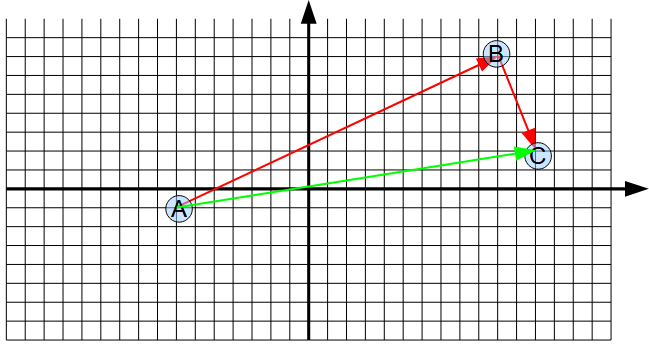 Pour additionner deux vecteurs, il faut appliquer le principe d'indépendance de chaque dimension. En effet ce qui arrive dans une dimension n'affecte pas une autre dimension, et réciproquement. Par exemple, un projectile avance à vitesse constante dans l'horizontale, mais décélère et accélère dans la verticale. Le mouvement dans chacune des dimensions est donc indépendant.
Pour additionner deux vecteurs, il faut appliquer le principe d'indépendance de chaque dimension. En effet ce qui arrive dans une dimension n'affecte pas une autre dimension, et réciproquement. Par exemple, un projectile avance à vitesse constante dans l'horizontale, mais décélère et accélère dans la verticale. Le mouvement dans chacune des dimensions est donc indépendant.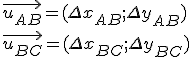
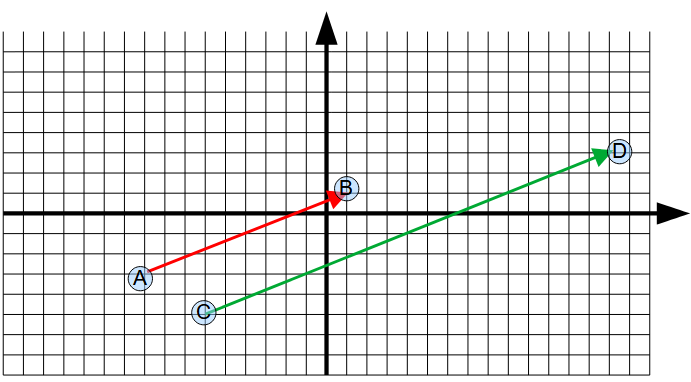 Multiplication par une constante
Multiplication par une constante Pour un produit vectoriel, le résultat est un troisième vecteur perpendiculaire aux deux premiers. Par exemple, un moment en physique est le produit vectoriel d'une force avec le vecteur position du point d'application par rapport à un axe. Si on connaît l'angle entre les deux vecteurs, alors la norme du produit vectoriel est donnée par l'expression suivante:
Pour un produit vectoriel, le résultat est un troisième vecteur perpendiculaire aux deux premiers. Par exemple, un moment en physique est le produit vectoriel d'une force avec le vecteur position du point d'application par rapport à un axe. Si on connaît l'angle entre les deux vecteurs, alors la norme du produit vectoriel est donnée par l'expression suivante: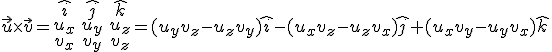
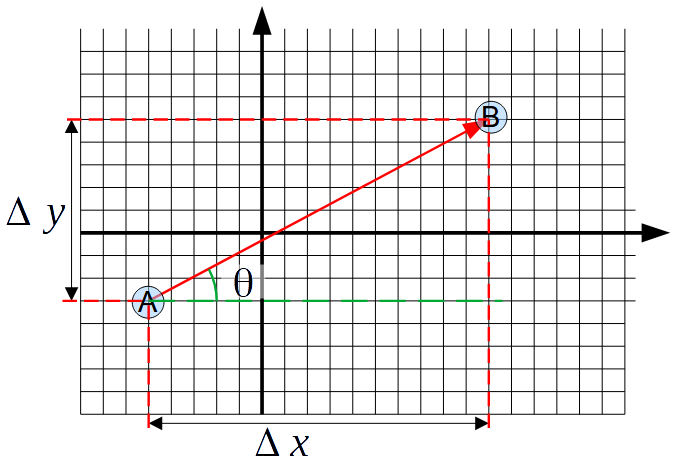 On peut calculer les différentes quantités décrivant les vecteurs en utilisant la trigonométrie. Tout dépend, comme toujours, de ce qu'on sait et de ce qu'on cherche.
On peut calculer les différentes quantités décrivant les vecteurs en utilisant la trigonométrie. Tout dépend, comme toujours, de ce qu'on sait et de ce qu'on cherche.