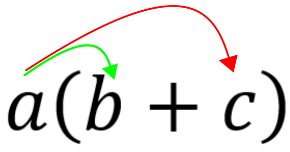Ici, c’est la distributivité de la multiplication qui s’applique : les parenthèses sont comme des boîtes, et le facteur \(a\) est simplement le nombre de ces boîtes. Il suit logiquement que :Nous avons revu les règles élémentaires d’opération. Passons à la manipulation d’expressions.
Une expression contenant des nombres et des lettres nécessite parfois d’être manipulée. Par manipulée, on entend réécrite dans une manière qui paraît plus intelligible ou solvable. Par exemple, il peut paraître nécessaire de se débarrasser de parenthèses dans une expression.
\[a\left( b + c \right)\]
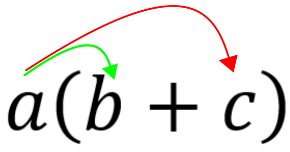Ici, c’est la distributivité de la multiplication qui s’applique : les parenthèses sont comme des boîtes, et le facteur \(a\) est simplement le nombre de ces boîtes. Il suit logiquement que :
\[a\left( b + c \right) = \text{ab} + \text{ac}\]
Comme on a vu qu’une division était la même chose qu’une multiplication, on en déduit :
\[\frac{a + b}{c} = \frac{a}{c} + \frac{b}{c}\]
Si ce sont deux boîtes qui se multiplient, alors les choses ne sont pas plus compliquées – juste plus longues.
\[\left( x + a \right)\left( x + b \right) = x^{2} + \text{xb} + \text{xa} + \text{ab}\]
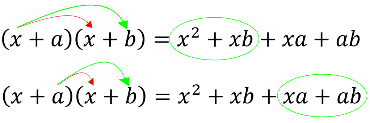Ici, on a d’abord multiplié la deuxième boîte par \(x\), puis par \(a\) et, comme \(x\) et \(a\) s’ajoutent, ajouter les deux.
On en profite pour découvrir deux identités remarquables – une manière de réécrire une expression entière :
\[\left( x \pm a \right)^{2} = \left( x \pm a \right)\left( x \pm a \right) = x^{2} \pm 2\text{ax} + a^{2}\]
\[\left( x + a \right)\left( x - a \right) = x^{2} - a^{2}\]
Il y en aura d’autres – il serait bon de commencer à en dresser une liste.
La factorisation est l’opération inverse du développement, mais on l’utilise pour les mêmes raisons : réécrire une expression pour qu’elle soit plus simple à lire.
La factorisation revient à trouver le facteur commun à deux nombres ou plus.
\[\text{ax} + bx^{2}\]
Ici, les deux termes ont au moins un terme \(x\). On peut donc diviser les deux termes par \(x\) et multiplier la parenthèse entière pour ne pas changer la valeur de l’expression.
\[x\left( \frac{ax}{x} + \frac{bx^{2}}{x} \right) = x\left( a + bx \right)\]
On a factorisé le \(x\).
On notera que les identités remarquables notées précédemment permettent parfois de factoriser des expressions pas forcément faciles à factoriser à première vue. C’est bien là leur utilité…