Pour voir la vidéo de ce cours, c’est par ici.

Si une expression est une phrase mathématique, une équation est une phrase qui veut dire quelque chose. Et elle dit quelque chose de simple : ce qui est à gauche du signe égal est égal à ce qui est à droite.

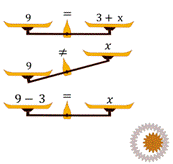Une équation est donc une phrase incluant des lettres, nombres et opérateurs, séparés par un signe égal.

Le plus souvent, lorsqu’on parle d’équation, on parle aussi d’inconnue. Et en général, l’inconnue, on veut la connaître. S’il existe, pour certains cas simples, des trucs (par exemple, le produit en croix), il est bon de comprendre la mécanique de la résolution d’équation en étudiant son algorithme et sa logique. La logique est toujours la même : ce qui est à gauche du signe égal est égal à ce qui est à droite, et doit le rester.

Algorithme

Un algorithme est une série d’instructions qui se suivent. Par exemple, l’algorithme de l’habillement contient entre autres les instructions mettre ses sous-vêtements, passer sa veste et mettre son pantalon. L’ordre dans lequel on suit ces instructions est important – sinon, on se retrouve avec le slip par-dessus le pantalon. Ce n’est donc pas une simple liste à suivre, mais une procédure qui demande un peu de réflexion.

La base de l’algorithme est dans le signe égal : ce qui est à gauche est toujours égal à ce qui est à droite. Si on ajoute des choses à gauche, on doit aussi les ajouter à droite ; si on en retire d’un côté, on doit aussi les retirer de l’autre.

Donc, allons-y :

1. Identifier l’inconnue

Parfois, l’inconnue s’appelle , parfois c’est autre chose. Et parfois, surtout en physique, l’équation entière est composée de lettres. Dans ce cas aussi, résoudre signifie simplement isoler l’inconnue.

2. Rassembler le ou les termes contenant l’inconnue d’un côté du signe égal, le reste de l’autre ; simplifier

Pour rassembler, il faut parfois passer un terme d’un côté à l’autre. Il faut alors le retirer des deux côtés, ou l’ajouter, ou le diviser, le multiplier… toujours aux deux côtés du signe égal.

3. Si une opération est faite sur l’inconnue, prendre sa réciproque

C’est quoi ça, la réciproque ? On va voir ça dans un instant…

4. Répéter la dernière étape jusqu’à ce que l’inconnue soit isolée

C’est généralement visible lorsqu’on arrive à ce stade : l’inconnue est toute seule d’un côté du signe égal…

5. Calculer l’autre côté

Une bonne habitude à prendre : garder tous les calculs pour la fin.

Réciproques

La réciproque d’une opération est l’opération qui permet de revenir à un état précédent.

Laissez-moi le temps d’expliquer…

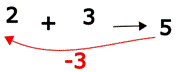Supposons que nous avons ajouté 3 à 2. Nous avons maintenant 5. La réciproque de l’opération qu’on vient de faire devrais nous permettre de revenir à 2. Cela signifie retirer 3. La réciproque de l’opération ajouter 3 est donc retirer 3.

Supposons maintenant que nous avons divisé 12 par 4. Nous avons maintenant 3. Pour revenir à l’état précédent (12), il faudrait multiplier par quatre. La réciproque de l’opération diviser par 4 est donc multiplier par 4.

Prendre la réciproque d’une opération permet d’isoler l’inconnue de n’importe quelle opération qui est faite sur elle – et, bien sûr, d’effectuer la même opération de l’autre côté. Encore faudrait-il connaître les réciproques de toutes les opérations… Listons-en certaines dans le détail :

Addition :

La réciproque de l’addition est donc la soustraction.

Soustraction :

La réciproque de la soustraction est donc l’addition.

Multiplication :

Division :

On voit que la multiplication et la division sont les réciproques de l’une sur l’autre.

Exposant :

ou

ou

Peut-être que cette écriture est encore un peu absconse. Pour simplifier l’écriture, on peut dire que la réciproque d’un exposant est la racine de cet exposant.

Et inversement :