Pour la version en vidéo, c’est par ici.
Exemple d’équation simple
Prenons un exemple d’équation simple – par simple, on entend que l’inconnue peut être isolée.
On souhaite faire une bouteille composée d’un cylindre et
d’un cône. On sait que le volume doit être de 1 litre (![]() )
et que les hauteurs du cône et du cylindre sont égales à
)
et que les hauteurs du cône et du cylindre sont égales à ![]() ,
pour une hauteur totale de
,
pour une hauteur totale de ![]() .
Quel doit être le rayon ?
.
Quel doit être le rayon ?
Pour répondre à cette question, il faut d’abord connaître les formules pour le volume d’un cône et d’un cylindre. Heureusement, notre prof de maths favori ou, plus probablement, Internet nous dit :
![]()
![]()
Nous savons que le volume entier (cylindre plus cône) doit
être égal à ![]() .
On écrit donc :
.
On écrit donc :
![]()
Nous connaissons la hauteur du cylindre et du cône –
simplement ![]() ,
donc l’équation se simplifie :
,
donc l’équation se simplifie :
![]()
Par chance, l’expression peut se simplifier encore. Il ne reste plus qu’à la résoudre :
![]()
On divise par quatre et on multiplie par trois les deux côtés :
![]()
On divise les deux côtés par ![]() :
:
![]()
Et on prend la racine carrée des deux côtés :
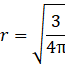
Problématiques
Un problème de colis fragile qui glisse sur une pente : lourd en physique, lourd en résolution d’équations…
Beaucoup plus simple, l’utilisation d’une feuille de calcul pour résoudre une équation trop difficile à résoudre : le tireur de paintball.