Pour la version en vidéo, c’est par ici.

Equations du second degré

Avant de nous attaquer aux équations du second degré, attardons-nous sur le cas où l’inconnue est au carré :

La solution est simple : il suffit de diviser les deux côtés par , puis de mettre les deux côtés sous une racine carrée.

Mais ce n’est pas tout à fait vrai. En fait, il existe deux solutions pour cette équation.

Prenons un exemple :

Si je place le résultat dans l’équation de départ, j’obtiens en effet 8 :

Mais j’obtiendrais le même résultat avec :

Donc, il y a deux solutions à cette équation : et . On écrit donc en fait :

Et ceci est vrai pour tous les exposants s’ils sont des chiffres pairs (2,4,6, etc.). On peut en déduire une nouvelle règle générale :

Pour , la solution est , où est un nombre entier.

Cela étant établi, commençons à parler un peu des équations du second degré.

Une équation du second degré est une équation dans laquelle l’inconnue apparaît deux fois : une fois sous la forme de , et une fois sous la forme de . Prenons d’abord la forme la plus simple.

Dans ce cas, on peut séparer les termes de part et d’autre du signe égal :

On peut diviser les deux côtés par :

Et résoudre enfin :

Ce n’était en fait pas si compliqué que ça.

Ça devient un peu plus compliqué s’il y a un terme constant ajouté à tout ça :

En effet, on ne peut plus séparer les termes – en mettre un à gauche du signe égal, l’autre à droite, et ils sont seuls chacun de leur côté. Quoiqu’on fasse, il y aura toujours ce dans le passage.

Lorsque nous parlerons des dérivées, nous verrons qu’il y a une solution assez simple à ce problème. Mais nous pouvons aussi utiliser un peu de géométrie.

Pour plus tard, je vais écrire cette équation de manière un peu différente :

J’ai changé certaines lettres, mais nous avons bien toujours la même situation : un terme qui multiplie , un qui multiplie et une constante.

Méthode 1 : factorisation

Avant de décrire comment trouver la forme factorisée d’une équation de la forme , voyons en quoi cela pourrait être avantageux.

La forme factorisée d’une équation du second degré est comme suit :

Imaginons que le premier terme entre parenthèse soit égal à zéro :

Comme n’importe quoi multiplié par zéro donne zéro, on a :

Donc, si on trouve la valeur de qui transforme le premier terme entre parenthèse en zéro, on aura une solution de l’équation du second degré :

C’est une équation simple à résoudre :

Et pour la deuxième solution, on fait la même chose au second terme entre parenthèses :

Simple, n’est-ce pas ?

Le problème, c’est que pour trouver la forme factorisée, il va falloir réfléchir.

Tout d’abord, entendons-nous bien : on veut passer de ça :

A ça :

J’ai coloré les différentes constantes pour insister sur un point : ce sont les mêmes lettres, mais ce ne sont pas les mêmes nombres.

Le plus simple serait de transformer la deuxième forme en la première forme pour voir les équivalences. Heureusement qu’on a revu la distributivité dans un chapitre précédent, hein ?

On réorganise tout ça de manière à avoir un facteur de , un facteur de et une constante :

On compare avec l’autre forme :

Il saute aux yeux que :

Ce serait très bien si c’était , et qu’on cherchait. Mais c’est , , et qu’on cherche. Heureusement qu’on a revu les systèmes d’équations dans un chapitre précédent, non ?

Non. Le problème est que nous avons quatre inconnues, et seulement trois équations. Heureusement qu’on a revu les identités remarquables, n’est-ce pas ?

Reprenons l’équation qu’on a à notre disposition :

On divise tout par , et on crée donc de nouvelles constantes et :

Ce qui nous donne la même équation sous plusieurs formes :

↔

↔

↔

Il semble clair maintenant en comparant les équations que la stratégie va avoir plein de si…

Pour :

· si , alors et

· si , alors et

· si , alors et

Par exemple :

On a l’équation .

On calcule :

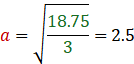
On calcule :

On vérifie si :

C’est donc le premier si qui s’applique :

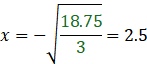
On vérifie, et ça marche :

Cela fait une procédure assez complexe, en fin de comptes : il ne faut pas se rater dans une des étapes.

Mais le vrai problème avec cette méthode, c’est : et si ce n’était pas le cas ? Et si et ? Alors il va falloir utiliser la deuxième méthode.

Méthode 2 : compléter le carré

On reprend la forme de notre équation du second degré :

Divisons tout par .

Et passons le dernier terme de l’autre côté du signe égal :

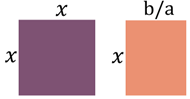Maintenant, nous pouvons représenter cette situation en utilisant des carrés et des rectangles :

Le premier terme est la surface d’un carré de côté . Le second terme est la surface d’un rectangle dont un côté est égal à , l’autre à .

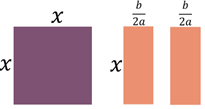Le troisième terme est… une surface négative ? Peu importe pour le moment, on reviendra plus tard sur ce point. Et de toutes façons, je n’ai représenté ici que le côté gauche. Parce qu’une surface négative, je ne sais pas ce que sais. Ça fait un peu peur, en fait…

Soit. Divisons le rectangle en deux parties égales et repositionnons-les. Ça fait deux petits rectangles de longueur et de largeur en plus d’un carré de côté .

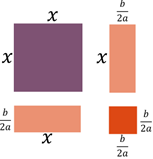On voit que si on ajoute un petit carré au côté gauche, on obtiendrait un carré complet. Le côté de ce petit carré mesure .

On calcule les aires, et on ajoute celle du petit carré. Pour respecter le signe égal, on ajoute le même petitcarré au côté droit.

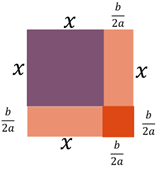On remplace alors tout le côté gauche par l’aire du grand carré.

On en profitera pour reconnaître une des identités remarquables dont on a parlé plus tôt…

La résolution est alors assez simple : mettre les deux côtés sous une racine carrée, et résoudre pour … en prenant bien en compte le fait qu’il pourrait y avoir deux solutions.

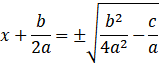
On peut réécrire tout ça d’une manière plus canonique – les ouvrages de mathématiques aiment utiliser la même forme :

Cette formule est tellement utilisée qu’on lui a donné un nom : la formule quadratique. Cela dit, elle est un peu intimidante, donc on a développé une procédure d’application :

1. Calculer le déterminant ; on l’appelle déterminant parce qu’il détermine combien de solutions une équation du second degré a.

2. Si le déterminant est négatif (vous vous rappelez de la surface négative ?), alors il n’existe pas de solution réelle. Il existe des solutions imaginaires, mais ce sera pour une autre fois…

3. Si le déterminant est supérieur ou égal à 0, alors il existe une ou deux solutions, données par la formule quadratique (une fois avec le plus, une fois avec le moins) :

Spoiler :

Nous avons développé deux méthodes de résolution d’une équation du second degré. La première marche parfois, la seconde toujours. Devinez un peu laquelle vous utiliserez toujours…

Problématiques

Une problématique qui applique Thalès et la résolution d’une équation du second degré pour trouver le nombre d’or.