Pour une version vidéo de ce cours, c’est par ici.

Distance, surface ou section

Une distance est la différence entre deux positions. Ces deux positions sont déterminées par un référentiel, c’est-à-dire un espace dont on a déterminé arbitrairement une origine. Par exemple, lorsqu’on mesure quelque chose, on commence classiquement par . On a donc déterminé notre origine comme étant égale à 0.

Mais on aurait pu utiliser une autre origine. Par exemple, on peut mesurer une personne, puis mesurer cette même personne avec un chapeau. La hauteur du chapeau sera simplement la différence entre la personne avec le chapeau et la personne sans le chapeau.

Formellement, on écrit une distance comme étant le delta entre deux points. Bien sûr, cette distance peut être une longueur, largeur, hauteur… mais aussi un rayon ou même un angle ! En effet, on peut utiliser un système de coordonnée qui s’applique à la situation étudiée :

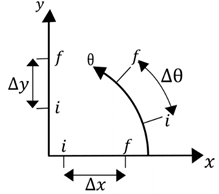Coordonnées cartésiennes :

Pour des formes qui peuvent être décrites avec des distances et :

Longueur

Largeur

Coordonnées polaires :

Pour des formes qui peuvent être décrites avec une distance d’un axe de rotation et un angle :

Rayon

Angle

Dans la pratique, on utilisera rarement le delta des différentes dimensions – généralement, on commence une mesure à 0. Mais il sera important de s’en rappeler en physique, et aussi lorsque nous aborderons les dérivées.

Formes usuelles

Une surface ou section est le produit de deux dimensions qui sont perpendiculaires l’une à l’autre. En coordonnées cartésiennes, cela revient à multiplier une longueur par une largeur.

Cas particulier : le carré, pour lequel la longueur est égale à la largeur (un côté ) :

Un triangle rectangle est un rectangle qu’on a coupé en deux. Sa surface est donc :

En coordonnées polaires, les choses sont un peu plus avancées. Pour bien comprendre ce qui va suivre, il est peut être nécessaire de revenir sur la définition de .

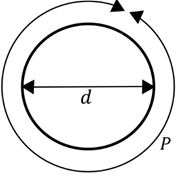Lorsqu’on forme un cercle avec une corde, le ratio de la longueur de la corde par le diamètre du cercle est toujours le même nombre, quelle que soit la taille de la corde : .

Si je choisis d’exprimer cela sous forme de formule, j’obtiens :

Ce nombre est donc un nombre sans dimensions. On parlera toutefois de radians lorsqu’on mesurera un angle. Une unité alternative et plus courante est le degré, mais il faut savoir que .

En résolvant cette équation pour le périmètre , j’obtiens la formule pour le périmètre d’un cercle. Exprimé en termes du rayon :

Reconnaissant que est l’angle d’un cercle, on peut en déduire la formule pour calculer un arc de cercle :

Attention encore : l’angle dans cette formule est en radians, pas en degrés.

La surface étant le produit entre deux dimensions, on devine qu’un arc de disque (plus communément appelé secteur) est le produit du rayon avec un arc de cercle, mais attention : on calculerait en fait deux fois la surface. Il faut donc tout diviser par deux.

Et pour un disque complet, pour lequel l’angle est :

Je reviendrai sur ce calcul quand on parlera des intégrales de surface.