Pour une version vidéo de ce cours, c’est par ici.

Fonctions simples

Une fonction est une machine mathématique qui prend un nombre en entrée et sort un autre nombre en sortie. En langage mathématique, on dit qu’elle prend une valeur et restitue une image .

Il est important de noter qu’une fonction n’est pas directement similaire à une équation. En effet, une équation donne un résultat pour une variable . Une fonction donne un ensemble d’images pour un ensemble de variables. C’est une subtilité qu’il est important de garder en tête afin d’opérer la transition de fonction à équation sans perdre le fil.

Si l’ensemble de variables peut être infini, on précisera souvent sur quel intervalle est défini. On écrira alors :

où

Le symbole veut dire appartient, et les crochets indiquent un intervalle entre une valeur de initiale et une valeur finale. Traduit en français : la fonction est définie pour des valeurs appartenant à un intervalle.

On notera qu’on épelle f de x, c’est-à-dire fonction de la variable .

Nous étudierons cinq fonctions simples, qui sont toutes écrites de la même manière :

Image et antécédent

Lorsqu’on calcule l’image d’une variable , il est usuel d’écrire pour le résultat, ou même de le remplacer par .

Pourquoi ? A cause des graphiques.

La représentation graphique est une courbe qu’on appellera ou dans un espace en deux dimensions et . Il n’existe donc pas une valeur particulière pour : c’est un ensemble de valeurs. En revanche, pour chaque valeur de , il existe une valeur qui lui correspond, et qui est donnée par la fonction .

Clarifions ce point par l’exemple :

J’ai une fonction et une variable en particulier que j’appellerai . Lorsque je calcule l’image, j’écris :

Cette image que j’obtiens correspond à une valeur sur l’axe , que j’appellerai . J’écris alors :

A la fin, j’écrirai directement :

Et j’ai transformé la fonction, une machine à donner un nombre infini de valeurs, en équation, une expression qui lie un nombre spécifique à un autre nombre spécifique .

Si c’est cette valeur que je connais, je peux calculer l’antécédent – la valeur de qui donne cette image en particulier. Il s’agit alors d’une simple équation à résoudre :

Ou, écrit autrement :

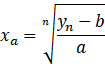
Cinq fonctions simples :

Pour chacune des fonctions simples ci-dessous, j’ai créé des appliquettes Géogebra. Dans la description, vous trouverez des liens vers ces appliquettes pour manipuler les quantités et et voir leur influence.

Fonction affine :

Une fonction affine ressemble à une ligne droite. On notera :

· que l’ordonnée à l’origine, c’est-à-dire , est égale à

· que si , la courbe est décroissante ; que si , la courbe est croissante

Fonction carrée :

Une fonction carrée ressemble à une parabole. On notera :

· que l’ordonnée à l’origine, c’est-à-dire , est égale à

· que si , la parabole est ouverte vers le bas ; que si , la parabole est ouverte vers le haut

On dit de la fonction carrée qu’elle est paire, c’est-à-dire que .

Fonction cube :

Une fonction cube ressemble à deux paraboles, une positive, l’autre négative. On notera :

· que l’ordonnée à l’origine, c’est-à-dire , est égale à

· que si , la courbe vient de l’infini positif et va vers l’infini négatif ; que si , la courbe vient de l’infini négatif et va vers l’infini positif

On dit de la fonction cube qu’elle est impaire, c’est-à-dire que .

Fonction racine :

Ou, écrit d’une manière qui vous sera peut-être plus familière :

Une fonction racine… ne ressemble à rien de particulier. On notera :

· que l’ordonnée à l’origine, c’est-à-dire , est égale à

· que cette fonction ne prend pas de négatif

· que si , la courbe est décroissante ; que si , la courbe est croissante

Fonction inverse :

Une fonction inverse semble créer deux courbes différentes séparées par l’axe des ordonnées. On notera :

· que cette fonction n’est pas définie à l’origine - semble égal à l’infini positif et l’infini négatif en même temps.

· que est la valeur vers laquelle cette fonction tend vers les infinis – on l’appelle alors l’asymptote, la valeur que la fonction ne dépasse jamais.