Pour un version en vidéo de ce cours, c’est par ici.

Trouver 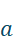et

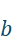
Il peut arriver qu’on ait des informations sur une fonction, mais pas la fonction elle-même. Il est alors nécessaire de trouver la fonction. Oui, ça peut sembler évident, mais il est bon de le rappeler à certains : en général, ce qu’on cherche, c’est ce qu’on ne connaît pas…

Trouver la fonction revient à identifier et calculer et .

Pour identifier , il suffit de savoir la forme de la fonction : affine, carrée, cube, etc. C’est notre premier élément d’information.

Pour trouver et , il faut mettre en place un système d’équations. En effet, s’il y a deux inconnues, il faut deux équations.

Ces deux équations nécessitent les coordonnées de deux points par lesquels passe la courbe représentant la fonction. Pour rappel : les coordonnées d’un point sont un set de deux nombres entre parenthèses, séparés par un point-virgule.

Supposons les coordonnées d’un point et d’un point :

On intègre ces coordonnées dans la fonction :

On peut résoudre la première équation pour :

… et mettre le résultat dans la deuxième équation :

Il ne reste plus qu’à résoudre pour :

Ce qui veut dire ici factoriser , et résoudre :

Pour trouver , il suffit d’insérer ce qu’on a trouvé dans la première ou la seconde équation, et de résoudre pour  :

ou

Incidemment, on a le choix entre deux équations pour trouver . Même si ce n’est pas nécessaire, il est malin de calculer les deux : si on obtient deux fois le même résultat, on a tout juste. Sinon : on a dû commettre une erreur quelque part, et il faut la trouver…

Par exemple :

J’ai une fonction qui ressemble à une fonction racine. Elle passe par les points et .

J’insère les coordonnées de ces deux points dans deux fonctions racine. J’obtiens un système d’équations.

Je résous la première équation pour :

Et je mets le résultat dans la deuxième équation :

Je résous le tout pour :

Et je mets le résultat dans les deux équations initiales pour trouver :

Je résous les deux équations pour – ça devrait me donner le même résultat :

Ayant identifié les deux inconnues, je peux enfin écrire la fonction que la courbe représente :