Dérivées et points d’intérêts

On a vu les fonctions, ce qu’on peut faire avec les fonctions, et même comment trouver certaines fonctions simples.

Mais comment peut-on analyser une fonction ?

La dérivée d’une fonction est une fonction qui décrit son évolution.

(…)

Ce n’est pas très éclairant, ça…

La dérivée d’une fonction est une fonction qui décrit l’évolution de la fonction .

Plus précis, et cela inclut la notation f prime, mais pas plus clair…

Prenons l’exemple d’une pente. Sur la route, une pente de 7% signifie une pente raide, et que si on la descend il faut utiliser le frein moteur, ou que si on la monte il ne faut pas rester derrière un camion.

Le 7% signifie que pour 100 mètres parcourus à l’horizontale, 7 mètres sont parcourus à la verticale.

Eh bien, la dérivée d’une fonction, c’est l’estimation de la pente de cette fonction à chaque valeur de . Et de toutes ces estimations on fait une nouvelle fonction qu’on appellera .

Pour une simulation de la dérivée d’une fonction carrée, cliquer sur le lien suivant : dérivée d’une fonction carrée.

Je pense que c’est un peu plus clair. Ca le sera peut-être plus avec des exemples.

La dérivée d’une constante est 0 : une constante, par définition, ne change pas, n’a pas de pente.

Noter qu’on disait f de x pour la fonction ; pour la dérivée, on dira f prime de x.

La dérivée d’une fonction linéaire (passant par l’origine) est simplement la pente de la fonction :

Pour une fonction carrée, cela devient un peu plus compliqué : la pente n’arrête pas de changer. On peut faire l’approximation de calculer la pente entre des paires de points très rapprochées tout le long de la courbe. On obtient alors une collection de points qui forme une fonction affine. On peut en trouver facilement la forme :

On note alors à nouveau un motif : la dérivée de , c’est . La dérivée de , c’est . On devine que la dérivée de , c’est … ?

Bingo.

On en déduit une formule permettant de trouver la dérivée d’une fonction simple ou d’un polynôme (après tout, un polynôme n’est jamais qu’une somme de fonction simples) :

Pour ,

On pourrait passer à un moment pour construire une liste des dérivées de toutes les fonctions simples (affine, carrée, cubique, etc.), mais ce serait fastidieux et, à la fin et à mon avis, inutile : mieux vaut appliquer cette formule. Mais n’allez pas croire qu’il serait complètement inutile de vérifier :

· sur une feuille de calculs, dresser le tableau de valeurs d’une fonction avec un petit pas (au maximum 0.1)

· dans une colonne, calculer la pente entre les deux premiers points de la fonction ; pour rappel, la formule pour calculer la pente d’une fonction de type  :

Oui, j’ai dû utiliser la lettre pour l’exposant parce que la lettre était prise pour le rang…

· copier la formule jusqu’à l’avant dernière cellule de la fonction

· faire un graphique, et deviner quelle fonction décrit la dérivée

A coup sûr, la fonction sera donnée par la formule que j’ai donnée. Si ce n’était pas le cas, en tant que prof de maths, je serais bien embêté…

Intéressons-nous plutôt à ce à quoi cela pourrait bien servir, une dérivée.

La réponse est dans comment on l’a trouvée : c’est une mesure de l’évolution de la fonction. SI la dérivée est négative, la fonction décroît ; si elle est positive, elle croît.

Et si la dérivée est égale à 0 en un point , alors la fonction atteint un extremum à ce point.

La dérivée permet donc de trouver les coordonnées de l’extremum d’une fonction.

Tout cela serait très bien si seulement on savait ce que c’était, un extremum.

Un extremum est un maximum ou un minimum.

Maintenant, on sait.

Prenons un exemple.

On a un polynôme du second degré :

On a compris que la dérivée nous permettrait de trouver les coordonnées de son extremum. On trouve donc la dérivée :

Nous savons que là où la dérivée est égale à zéro, cela correspond à la coordonnée horizontale de son extremum. On égalise la fonction à zéro, et on résout pour :

La coordonnée de l’extremum est donc égale à -25. Pour trouver sa coordonnée , il suffit d’insérer ce résultat dans la fonction originale :

Les coordonnées de l’extremum de cette fonction sont donc :

Pour savoir s’il s’agit d’un maximum ou d’un minimum, il suffit de regarder le signe de : s’il est négatif, la parabole est ouverte vers le bas. Il s’agit dont ici d’un maximum.

L’utilité des dérivées et de leurs réciproques, les primitives, va bien plus loin que la découverte de points d’intérêts comme le ou les extrema d’une fonction. Par exemple, elles peuvent servir à (re)découvrir la formule quadratique.

On note que l’extremum d’un polynôme du second degré se trouve à une distance égale à de ses racines – là où la courbe croise l’axe des abscisses. Si on pouvait trouver la valeur de , on pourrait trouver une formule qui nous permettrait de calculer les coordonnées de ces racines.

Tout d’abord, trouvons une formule pour l’extremum, et appelons sa coordonnée horizontale  :

La coordonnées verticale est obtenue simplement en intégrant dans la fonction originale :

Mais ce qui nous intéresse, c’est . Prenons le cas où on ajoute :

Et nous savons qu’à , la fonction, croisant l’axe des abscisses, est égale à zéro :

Développons :

Les choses se simplifient, des termes s’annulent :

Et se simplifient encore…

On peut enfin résoudre pour :

Qu’on peut réécrire :

On finit de résoudre et on simplifie encore :

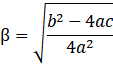
Pour trouver l’autre racine, il suffit de soustraire . La formule quadratique est donc :

Ce qui nous fait une deuxième preuve de la formule quadratique (la première était dans la section sur les équations du second degré).

C’est sympa, les dérivées.

Problématiques

Le problème du cascadeur : trouver la vitesse minimale d’un véhicule pour qu’il puisse sauter d’une rampe et atterrir sur une plateforme en hauteur.