Pythagore

Le théorème de Pythagore est suffisamment connu pour qu’on puisse se passer d’une explication.

Pourtant, je vais prendre le temps de l’expliquer.

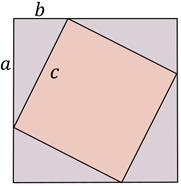
Imaginez deux carrés. Le plus petit est dans le plus grand mais penché, en sorte de former quatre triangles rectangles donc l’hypoténuse est égale au côté du plus petit des carrés.

Le côté du plus petit carré est noté ; les triangles, tous identiques, ont une base et une hauteur .

L’aire du grand carré est égale à l’aire du petit carré et des quatre triangles.

Mais l’aire du grand carré est aussi égale au carré d’un de ses côtés.

Les deux expressions étant égales, on les égalise.

On développe :

Et on résout pour ; les termes s’annulent :

Le carré de l’hypoténuse est égal à la somme des carrés de la base et de la hauteur d’un triangle rectangle. Nous avons prouvé Pythagore.

On en déduit les formules pour calculer le côté d’un triangle rectangle à partir des deux autres :

Sinus et cosinus

Un cercle peut être vu comme une collection de triangles dont l’hypoténuse est égale au rayon du cercle, et dont la base et la hauteur varient avec l’angle.

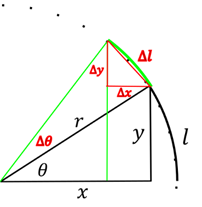Pour toute valeur de on sait de Pythagore que .

Toujours en utilisant Pythagore, on peut faire l’approximation, pour des petits changements de et de , de l’arc de cercle comme étant égal à .

En ajoutant ces petites longueurs les unes aux autres, on obtient un cercle complet. En divisant par , comme , on obtient l’angle.

J’ai simulé ce que je viens de décrire sur une feuille de calculs ; calculé , la valeur de pour chaque écart ; fait la somme des pour chaque valeur de et divisé par pour obtenir l’angle ; et enfin calculé, pour chaque angle , le ratio de sur l’hypoténuse . J’ai fait un graphique de la fonction de ainsi trouvé, et comparé avec…

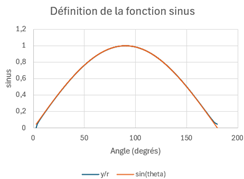On appellera le ratio de la hauteur d’un triangle rectangle (le côté opposé à l’angle) avec son hypoténuse.

Comme on peut le voir, le ratio de l’opposé sur l’hypoténuse renvoie toujours les mêmes valeurs, quelle que soit l’hypoténuse. Et mon approximation de cette fonction de fonctionne plutôt bien.

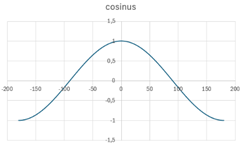On peut comparer ensuite l’angle avec le ratio de la base avec le rayon. Là aussi, on obtient toujours les mêmes valeurs, et quel que soit le rayon. On appellera le ratio de la base d’un triangle rectangle (le côté adjacent à l’angle) avec son hypoténuse.

Et enfin, parce que jamais deux sans trois, on appellera le ratio du sinus avec le cosinus d’un angle ou, plus directement, le ratio de la hauteur d’un triangle sur sa base.

Incidemment, on se rendra compte que la tangente d’un angle est la même chose que la pente d’une courbe en un point : le ratio de la distance verticale parcourue sur la distance horizontale parcourue.

Fort heureusement, on n’a pas besoin de calculer la longueur d’un arc de cercle chaque fois qu’on souhaite calculer un des côtés d’un triangle en utilisant l’angle : les fonctions trigonométriques sinus, cosinus et tangente sont programmées dans toutes les bonnes calculatrices et les feuilles de calculs qui se respectent.

Car ce sont des fonctions : des machines qui, lorsqu’on leur donne un nombre, sortent un autre nombre. L’argument – le type de nombre qu’on donne aux fonctions – d’une fonction trigonométrique est un angle. Le nombre qui en sort est, comme on l’a vu, le ratio de deux côtés d’un triangle rectangle.

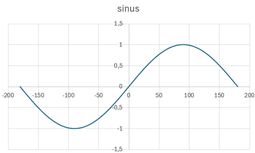Fonctions sinus

La fonction sinus est une fonction trigonométrique. A la différence des autres fonctions qu’on a vu jusqu’à maintenant, elle se répète – on dit qu’elle est périodique. On notera :

· qu’elle est égale à zéro à l’origine et à ()

· qu’elle atteint un extremum à ()

Pour une simulation de la fonction sinus, cliquer sur le lien suivant : fonction sinus. On notera que la simulation inclut la notion de déphasage, expliquée plus tard.

La réciproque de la fonction sinus, notée , s’appelle arc sinus.

Fonction cosinus

Une autre fonction trigonométrique, la fonction cosinus est elle aussi périodique. On notera :

· qu’elle atteint un maximum à l’origine et à

· qu’elle est égale à zéro à

La réciproque de la fonction cosinus, notée , s’appelle arc cosinus.

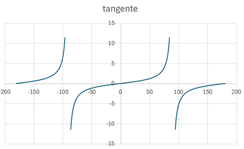
Fonction tangente

La fonction tangente, troisième des fonctions trigonométriques de base, est une fonction, vous l’aurez deviné, périodique. On notera :

· qu’elle est égale à zéro à l’origine

· qu’elle est indéfinie à

La réciproque de la tangente, notée , s’appelle arc tangente.

Les côtés d’un triangle rectangle

Une première utilisation des fonctions trigonométriques est dans le calcul des angles et des côtés d’un triangle rectangle. Cela peut sembler limité, jusqu’à ce qu’on se rendre compte que beaucoup de formes peuvent être ramenées à des triangles rectangles. Et la deuxième partie de ce chapitre est sur les vecteurs – les fonctions trigonométriques seront là aussi très utiles.

Supposons que nous connaissons un angle et l’hypoténuse d’un triangle rectangle. Avec ces informations et les définitions des fonctions trigonométriques, on peut calculer :

· l’adjacente à l’angle :

· l’opposée à l’angle :

Si vous connaissez l’angle et l’opposée à cet angle et que c’est l’adjacente que vous recherchez, la fonction tangente devient utile :

A ce stade, vous pouvez deviner comment obtenir un des côtés à partir de l’angle et d’un seul des côtés : résoudre pour l’inconnue.

Enfin, si c’est un des angles du triangle que vous recherchez, vous n’aurez que l’embarras du choix parmi les réciproques des fonctions trigonométriques :

Identités trigonométriques

Il y a beaucoup d’identités trigonométriques – vraiment beaucoup – dont certaines que nous verrons au fur et à mesure des besoins. Notons-en quelques-unes dès maintenant :

Supposons un triangle rectangle donc l’hypoténuse est égale à 1. L’adjacente à l’angle est donc simplement et l’opposée . Par Pythagore :

Noter au passage comment on écrit le carré d’une fonction trigonométrique : entre la fonction et son argument.

En regardant une représentation graphique des fonctions sinus et cosinus, on notera aussi que :

Enfin, toujours en comparant la représentation graphique des fonctions sinus et cosinus, on notera que la fonction cosinus est identique à la fonction sinus – juste décalée le long de l’axe horizontale, de 90° (). On en déduit :

Noter qu’on appelle cet angle de décalage déphasage.