Addition et soustraction :
Dans un espace en deux dimensions, un vecteur est représenté par une flèche qui pointe dans une direction. Ses coordonnées, car il y en a deux, sont respectivement le déplacement horizontal et le déplacement vertical.
\[\overrightarrow{v} = \left( \Delta x;\Delta y \right)\]
Un vecteur est donc une quantité mathématique qui contient trois informations :
une norme ou magnitude – une longueur
une direction (horizontal, vertical, et tout entre les deux)
un sens (vers un côté de la direction ou vers l’autre)
Le sens et la direction d’un vecteur sont contenus dans l’angle du vecteur, qu’on trouvera explicitement grâce à la réciproque de la fonction tangente.
\[\theta = \text{ta}n^{- 1}\left( \frac{\Delta y}{\Delta x} \right)\]
La norme, ou longueur, d’un vecteur peut être trouvée en utilisant Pythagore :
\[\left| \overrightarrow{v} \right| = \sqrt{\Delta x^{2} + \Delta y^{2}}\]
On note la norme d’un vecteur avec une ou deux paires de barres verticales :
\(\left| \overrightarrow{v} \right|\) ou \(\left| \left| \overrightarrow{v} \right| \right|\)
Pour des raisons pratiques, j’utiliserai la première représentation.
Comme pour tout objet mathématique, on peut appliquer des opérations aux vecteurs :
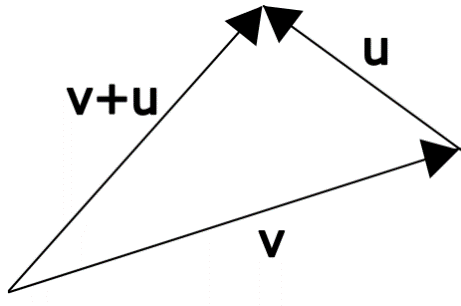
Addition et soustraction :
\[\overrightarrow{v} \pm \overrightarrow{u} = \left( v_{x} \pm u_{x};v_{y} \pm u_{y} \right)\]
L’addition de deux vecteurs donne un troisième vecteur.
Pour une simulation de l’addition de deux vecteurs, une appliquette Geogebra : addition de vecteurs.
Multiplication par un scalaire (un nombre qui n’est pas un vecteur) :
\[k\overrightarrow{v} = \left( kv_{x};kv_{y} \right)\]
Produit scalaire :
\[\overrightarrow{v} \cdot \overrightarrow{u} = v_{x} \times u_{x} + v_{y} \times u_{y}\]
Le produit scalaire entre deux vecteurs donne un scalaire.
Produit vectoriel (surface entre deux vecteurs) :
\[\overrightarrow{v} \times \overrightarrow{u} = v_{x}u_{y} - v_{y}u_{x}\]
Nous reparlerons dans le détail du produit scalaire et du produit vectoriel dans le chapitre sur les matrices.
Une application des vecteurs avec la trigonométrie est la représentation d’un déphasage entre deux quantités.
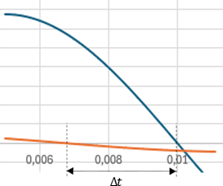Supposons que nous ayons deux fonctions trigonométriques dont l’une est en retard par rapport à l’autre :
\[f\left( t \right) = \text{Asin}\left( \omega t \right)\]
\[g\left( t \right) = \text{Bsin}\left( \omega t + \varphi \right)\]
La constante \(\omega\) étant la vitesse angulaire, elle est liée à la fréquence des fonctions :
\[\omega = \ 2\pi f\]
On représente ce retard par un angle \(\varphi\), dont le rapport avec le déphasage temporel \(\Delta t\) est :
\[\varphi= ω\ Δt\]
On représente alors la valeur maximale de la fonction \(f\left( t \right)\) par un vecteur allant à l’horizontale et la valeur maximale de la fonction \(g\left( t \right)\) par un vecteur allant à la verticale. La somme des deux vecteurs est un vecteur \(C\) dont l’angle est le déphasage \(\varphi\).
La représentation de fonction sinusoïdales par des vecteurs est très utile dans plusieurs domaines, notamment en électricité où le \(\cos\left( \varphi \right)\) est un ratio qui permet d’estimer le rendement d’un moteur ou d’une installation électrique.
Une simulation Geogebra du \(\cos\left( \varphi \right)\) est disponible en cliquant sur ce lien : Cos Phi.
Une preuve utilisant les concepts associés aux vecteurs du théorème d’Al Kashi.
Un classique des courts de mécanique : la règle et le marteau