Lorsqu’on multiplie une dimension par une surface, on obtient un volume. En connaissant certaines surfaces, on peut donc déduire certains volumes :

La surface d’un rectangle est le produit de sa largeur par sa longueur :

Le volume d’un parallélépipède (pavé droit) est donc simplement le produit de cette surface par la hauteur :

La surface d’un disque est le produit de par son sayon au carré :

Le volume d’un cylindre est simplement le produit de cette surface par la hauteur :

Si on se souvient de la surface d’un arc de disque :

… on peut deviner le volume d’un coin :

… à condition de se rappeler que l’angle ici est en radians, pas en degrés.

A partir de volumes, on peut déduire les volumes d’autres objets. Par exemple, le volume d’une pyramide dont la hauteur est égale à la moitié d’un des côtés de sa base. Si on dessine un cube, on voit qu’on peut le diviser en six parties donnant de telles pyramides. Le volume d’une pyramide est donc simplement :

Bien sûr, cette formule ne s’applique qu’à un cas particulier de pyramide. Il nous faudra des mathématiques un peu plus avancées pour aborder d’autres pyramides.

Pour une simulation de pyramide régulière dont la hauteur est égale à la moitié d’un des côtés de sa base : volume d’une pyramide régulière.

En conservant cette idée que, si une surface est le produit de deux dimensions, un volume est le produit de trois, et se souvenant qu’outre les coordonnées cartésiennes, il existe aussi des coordonnées cylindriques et des coordonnées sphériques, on devinera qu’il est possible de calculer le volume d’une sphère. Ce sera l’objet d’un chapitre plus tard, mais je laisserai ici, sans explication, la formule pour le volume d’une sphère :

Bon.

Ce n’est pas grand-chose, les applications sont assez limitées.

Cela dit, on peut aussi calculer des volumes en étant un peu malin.

La décomposition consistait à diviser une forme complexe en formes simples. Est-ce qu’on pourrait faire ça avec un cône ?

Quand on y réfléchit, un cône est une succession de cylindres dont le rayon change à mesure qu’on évolue le long d’un axe.

Introduisons un peu de langage de l’analyse ici.

On appelle un petit morceau de volume

Pour un cône, le rayon varie en fonction de la hauteur, et inversement. Si on le regarde de côté, l’apothème du cône est une fonction affine de la forme :

Je sais que le volume d’un cylindre est la base multipliée par la hauteur. Le volume d’un petit cylindre qui constitue le cône est donc la base est donc la base multipliée par une petite hauteur . Et la base a un rayon qui varie, de à 0.

Une fois que j’aurai calculé suffisamment de volumes, je n’aurai plus qu’à faire la somme pour trouver le volume d’un cône entier.

Et c’est ce que j’ai fait.

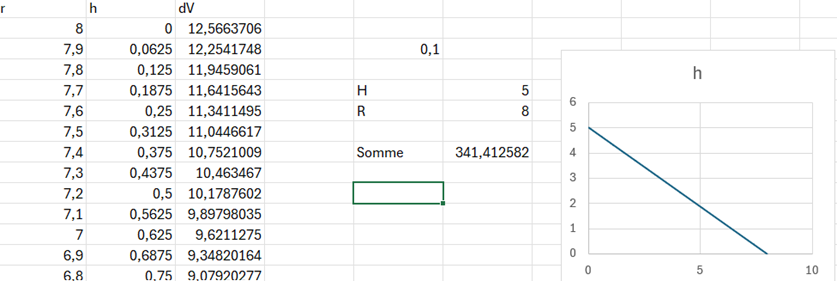
Dans la première colonne, j’ai écrit des valeurs pour de sa valeur à la base à zéro ; dans la seconde, j’ai écrit la fonction pour la hauteur en fonction du rayon. Et dans la troisième colonne, j’ai calculé les petits .

étant la variation de . La différence entre la valeur suivante et la valeur précédente.

J’ai calculé tout le long du rayon et fait la somme, et ça m’a donné un volume.

Bon, la vraie valeur donnée par la formule pour le volume d’un cône est autour de 335, mais c’est quand même assez proche.

Peut-être qu’en réduisant le pas, on trouverait quelque chose de plus proche de la réalité ?

Ce sera l’objet des intégrales dans l’espace.