On a vu que résoudre un système de deux équations est assez simple : résoudre la première équation pour une inconnue ; mettre l’expression ainsi obtenue dans la deuxième équation et résoudre pour la deuxième inconnue : mettre le résultat dans la première équation et résoudre pour la première inconnue.

Mais qu’en est-il de systèmes de trois, quatre… inconnues ?

C’est là que les matrices, des objets mathématiques, deviennent très utiles. Plus encore : c’est là que la technologie – et notamment les feuilles de calculs – vient à notre aide.

Le principe d’une matrice pour résoudre un système d’équations repose sur une idée simple : chaque équation linéaire peut être représentée sous forme d’une ligne droite. Là où les droites intersectent est un point dont les coordonnées correspondent aux solutions du système d’équations. Elargissant cette idée aux espaces à -dimensions, et vous avez un outil indispensable.

Composition d’une matrice

Une matrice est une grille qui contient des valeurs. Cette grille contient des lignes et des colonnes, dont les coordonnées sont données en indice et . Par exemple, voici une matrice carrée de dimensions (3 lignes par 3 colonnes) :

On peut donc représenter des ensembles de nombres qui sont liés les uns aux autres par une certaine construction. Par exemple, on peut représenter un vecteur par une matrice :

Propriétés

On peut ajouter des matrices les unes aux autres comme on ajoute des vecteurs les uns aux autres : en prenant chaque dimension à part.

Il en découle une première règle : on ne peut ajouter des matrices les unes aux autres que si elles ont les mêmes dimensions.

Pour la multiplication, ça va être un peu plus compliqué.

Tout d’abord, on ne peut opérer de multiplication qu’entre des matrices dont l’une à autant de colonnes que l’autre a de lignes.

Par ailleurs, le produit entre deux matrices a autant de lignes que la première matrice a de colonnes ; autant de colonnes que la première matrice a de lignes.

Essayons de représenter cette dernière règle :

Si je multiplie une matrice par une matrice , j’obtiens une matrice , c’est-à-dire un nombre.

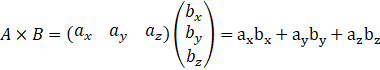
Oh. C’était en fait la définition du produit scalaire entre deux vecteurs. Bon à savoir.

Si je multiplie une matrice par une matrice , j’obtiens une matrice .

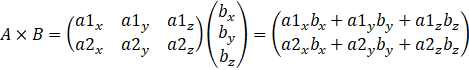
Et si je multiplie une matrice par une matrice , j’obtiens une matrice .

Et cætera.

Et quid du produit de deux matrices carrées de dimensions ?

D’une part, suivant la règle définie avant, le produit d’une matrice est une matrice . Une matrice de mêmes dimensions.

Ensuite, chaque terme de la matrice résultante est la somme des produits des termes de la ligne de la première matrice avec la colonne de la seconde.

Ce sera peut-être plus facile à comprendre avec l’écriture mathématique…

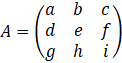
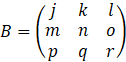
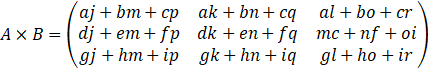
Il y a une petite possibilité que j’ai fait une faute de frappe en tapant tout ça. L’apprentissage de cette procédure est en fait… très kinesthésique, dans le mouvement :

· on multiplie la première ligne de la première matrice par la première colonne de la seconde ; on fait la somme ; ça donne le terme de la matrice résultante.

· on multiplie la première ligne de la première matrice par la seconde colonne de la seconde ; ça donne le terme de la matrice résultante.

· on multiplie la première ligne de la première matrice par la troisième colonne de la seconde ; ça donne le terme de la matrice résultante.

· on multiplie la deuxième ligne de la première matrice par la première colonne de la seconde ; ça donne le terme de la matrice résultante.

· on multiplie la deuxième ligne de la première matrice par la deuxième colonne de la seconde ; ça donne le terme de la matrice résultante.

· et ainsi-de suite jusqu’à la fin.

On l’aura deviné : la multiplication entre matrices n’est pas commutative.

On notera aussi que, sur une feuille de calculs, le produit de deux matrices est dans une simple fonction :

=PRODUITMAT(matrice 1 ; matrice 2)

Une feuille de calculs peut donc faire ce fastidieux calcul à notre place…

Une première application : réécrire un système d’équations sous forme de produit de deux matrices :

Peut se réécrire :

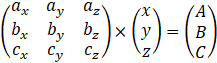
Si vous avez besoin d’une preuve, faites le produit des deux matrices à gauche du signe égal : vous devriez retrouver les trois équations de départ dans une matrice .