Déterminant d’une matrice

Le déterminant d’une matrice sert à…

Le déterminant d’une matrice prouve que…

Je ne sais pas.

Tout ce que je sais, c’est comment calculer le déterminant d’une matrice carrée. En utilisant la méthode des cofacteurs. Comme l’automobiliste lambda qui conduit sa voiture : je ne sais pas ni comment ni pourquoi ça marche, mais quand ça marche, ça roule.

Commençons par le déterminant d’une matrice :

Prenons le terme diagonalement opposé à . C’est . Ici, est appelé le mineur de . Donc, le terme diagonalement opposé à un terme de la matrice est le mineur de ce terme. On multiplie le premier terme par son mineur.

Le premier terme est dans la case de la matrice aux coordonnées . Cela signifie que et . Comme on doit multiplier ce qu’on vient de calculer par , et que … on ne fait rien.

A propos, le mineur d’un terme multiplié par où et sont les coordonnées du terme s’appelle le cofacteur du terme.

Passons au second terme : .

On multiplie ce terme par son mineur . Le premier terme est dans la case de la matrice aux coordonnées . Cela signifie que et . Comme on doit multiplier ce qu’on vient de calculer par , et que … on multiplie par ..

Et on fait la somme des deux cofacteurs.

Curieux, on essaye d’opérer la même procédure mais avec la deuxième ligne. Comme est aux coordonnées et est aux coordonnées

Ce qui revient au même. Donc, voilà : le déterminant est ce nombre qu’on obtient après une opération relativement complexe entre une ligne d’une matrice et tous les autres termes, et qui est le même quelle que soit la ligne qu’on utilise. Voilà une réponse bien inutile à la question c’est quoi, le déterminant d’une matrice…

Prenons maintenant une matrice .

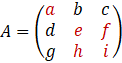
Cette fois, le mineur de n’est pas un nombre mais une matrice . Soit. Le premier terme de la somme que nous devons calculer est donc le produit de avec le déterminant d’une matrice . C’est bien, on a déjà vu comment calculer le déterminant d’une matrice :

Noter au passage qu’on note le déterminant d’une matrice comme une matrice entourée de deux barres verticales.

Maintenant, la suite. La matrice mineure est séparée par les termes en dessous du terme, mais ça forme quand même une matrice :

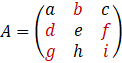
Cette fois, le calcul à faire est :

Et enfin :

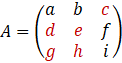
Et on fait la somme :

Résumons la procédure sous forme de procédure claire et de formule non moins claire :

· Pour chaque terme, identifier son mineur ; prendre le déterminant de ce mineur si nécessaire.

· Multiplier le déterminant par à la puissance de la somme des coordonnées du terme. On obtient son cofacteur.

· Multiplier le cofacteur par le terme.

· Une fois avoir fait tous les termes de la ligne, faire la somme des produits des cofacteurs avec leur termes.

Traduit en formule :

Rappel : est le mineur de .

Si vous pensiez que cette procédure est complexe et arbitraire, vous n’êtes pas le seul. Mais elle se tient : on peut l’appliquer aux autres lignes de la matrice et toujours trouver le même déterminant. On peut même suivre une colonne à la place d’une ligne, et encore trouver la même valeur.

Maintenant, imaginez que l’on doive appliquer cette procédure à une matrice . Le mineur de chaque terme serait une matrice dont il faudrait calculer le déterminant. Ce serait pour le moins fastidieux…

Heureusement, les feuilles de calculs ont une fonction bien pratique pour calculer le déterminant d’une matrice, et ce quelle que soit sa taille et pourvu qu’elle soit carrée :

=DETERMAT(matrice)

Voilà la deuxième fois que les feuilles de calculs vont faire les calculs pour nous…