Matrice inverse

Rappelons-nous quel était notre objectif : résoudre une équation à inconnues.

Déjà, nous avons vu que nous pouvons réécrire un système de trois équations sous forme de matrices :

…devient :

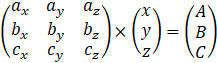
Appelons la première matrice , celle contenant les inconnues , et celle contenant les constantes . On obtient alors l’équation :

Normalement, pour résoudre cette équation, on doit multiplier les deux côtés du signe égal par l’inverse de la matrice. On obtiendrait alors :

La question est donc : comment trouver ?

Si c’était une équation simple, on devrait trouver le nombre qui, multiplié par le nombre qu’on cherche à faire passer de l’autre côté du signe égal, donnerait 1.

Ici, on cherche la matrice qui, multipliée par , donnerait la matrice unitaire (une matrice égale à 1).

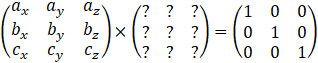
Vous pouvez vous amuser à multiplier n’importe quelle matrice par la matrice unitaire, et vous verrez qu’en effet, elle est égale à 1 : le résultat serait la matrice que vous avez multipliée par la matrice unitaire.

Sans plus d’explications, passons à la procédure pour trouver . Et pour faciliter la lecture, prenons une matrice .

Tout d’abord, on doit trouver la comatrice. La comatrice d’une matrice est une matrice qui contient les cofacteurs de la matrice . On se souvient de comment trouver les cofacteurs :

Donc, la comatrice de notre matrice est :

Maintenant, on prend la transposée de la comatrice. La transposée est simplement la matrice où les termes en haut à droite sont intervertis avec les termes en bas à gauche – les lignes sont maintenant des colonnes, les colonnes des lignes. Prenant un exemple avec une matrice :

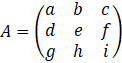
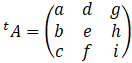
Donc, prenons la transposée de notre comatrice :

Et enfin, on divise tout par le déterminant de la matrice.

J’ai promis plus tôt que le produit d’une matrice avec son inverse donne la matrice unitaire. On va essayer ça :

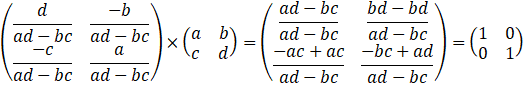
Tout cela fait une procédure à étapes multiples pour trouver l’inverse d’une matrice.

Incidemment, pour trouver l’inverse d’une matrice avec une feuille de calculs, la fonction est :

=INVERSEMAT(matrice)

Et voilà la troisième fois que la feuille de calculs fait tout le travail à notre place.