Produit vectoriel

Nous avons appris à calculer le déterminant, mais nous ne l’avons pas utilisé. Il faut dire que sa première utilisation réside dans l’assurance qu’il n’est pas égal à zéro. SI c’était le cas, il n’y aurait pas de solutions à notre système d’équations. Dit autrement, toutes les lignes représentant ces équations ne se croisent pas au même point.

C’est un peu limité, comme usage.

Heureusement, il y a une autre application du déterminant : le produit vectoriel.

Une application indirecte, toutefois. Rappelez-vous que le calcul du déterminant d’une matrice est un scalaire, alors que le produit vectoriel est le produit entre deux vecteurs qui donne un troisième vecteur. S’il est faux de dire que le produit vectoriel est le déterminant d’une matrice, il faut reconnaître qu’il y a une grande similarité.

Laissez-moi décrire ma définition et expliquer ce que tout cela veut dire ensuite.

Tout d’abord, les vecteurs. Supposons deux vecteurs :

Le produit vectoriel est le déterminant d’une matrice contenant les vecteurs unitaires , et , unitaires parce qu’ils ont tous une valeur numérique de 1 ; ils représentent chacun une des trois dimensions de l’espace. Les deuxième et troisième lignes sont les deux vecteurs dont on cherche le produit vectoriel :

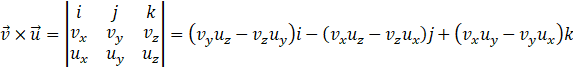
Notez que je privilégie la notation anglosaxonne pour le produit vectoriel, par habitude autant que parce que je ne trouve pas le code en Latex pour la notation francophone.

Ah, si, j’ai trouvé : c’est \wedge : . Peu importe.

Maintenant, qu’est-ce que c’est, le produit vectoriel, et en quoi est-il différent du produit scalaire ?

Le produit scalaire est la multiplication de deux vecteurs entre eux ; ce produit donne un scalaire, un nombre tout seul qui n’est pas un vecteur. Nous nous contenterons pour le moment de deux dimensions.

Notez comme on utilise un point pour symboliser la multiplication sans qu’on la confonde avec un produit vectoriel.

On se rappelle comment calculer les coordonnées d’un vecteur à partir de sa norme et de l’angle qu’il fait avec l’horizontale :

On en déduit le produit scalaire :

On peut factoriser :

Ici, il existe une identité remarquable qui va nous être très utile :

Je ne maîtrise pas vraiment la preuve de cette identité – je n’ai pas pris le temps de l’étudier – mais ça ne m’empêchera pas de l’utiliser ici. Si on admet que , c’est-à-dire que est l’angle entre les deux vecteurs :

Ce petit truc devient très utile quand on cherche à calculer le travail d’une force à un certain angle. Mais on laissera ça à la physique.

Mais aussi :

Donc, on peut trouver l’angle entre n’importe quels vecteurs si on connaît leurs coordonnées.

On pourrait continuer à trouver des nouvelles propriétés qui pourraient aider certains problèmes en géométrie. On pourrait remplir des pages. Mais passons au produit vectoriel.

Le produit vectoriel aussi aide beaucoup en géométrie (et en mécanique, surtout).

Le produit vectoriel est le produit de deux vecteurs entre eux. Le résultat est un troisième vecteur, et c’est là la différence avec le produit scalaire.

Prenons deux vecteurs : un qui va dans le sens de (), un autre qui va dans le sens de ().

Le produit vectoriel entre deux vecteurs est le déterminant de la matrice contenant les vecteurs unitaires et les deux vecteurs. Je l’ai déjà dit.

Ce qui nous donne le vecteur :

Intéressant : ce vecteur va dans le sens de (). Le produit vectoriel entre deux vecteurs donne donc un troisième vecteur qui est perpendiculaire aux deux autres.

Changeons la taille de ces vecteurs :

Intéressant encore : le produit vectoriel entre deux vecteurs semble donner la surface entre les deux vecteurs.

Ce serait certainement quelque chose à tester avec d’autres vecteurs et à représenter graphiquement, mais pour l’instant, répétons les deux propriétés du produit vectoriel :

· le vecteur obtenu est perpendiculaire aux deux autres

· sa norme est égale à la surface entre les deux vecteurs

Tout cela sera très utile lorsque nous parlerons de moment d’une force, de charges électriques mouvant dans un champ électrique… et de concepts physiques plus complexes que ça.

Incidemment, les mauvaises langues pourraient dire que j’ai passé trop de temps à expliquer comment calculer le déterminant alors que les feuilles de calculs le font pour nous. Eh bien, mauvaise nouvelle pour les mauvaises langues : il faut savoir calculer le déterminant manuellement pour pouvoir opérer le produit vectoriel. Ce n’est pas si compliqué, puisqu’il n’y a que trois dimensions de l’espace, et donc que le seul déterminant qu’on doit calculer est celui d’une matrice .