Surface et angle entre deux vecteurs

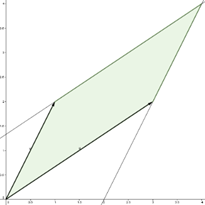Allez, prenons un exemple : calculons la surface et l’angle entre deux vecteurs.

On a deux vecteurs dans un espace en trois dimensions :

Le produit vectoriel entre ces deux vecteurs est donné par le déterminant de la matrice :

Tout cela ce simplifie gentiment :

Le vecteur résultant de ce produit vectoriel a donc les coordonnées :

Et la norme de ce vecteur est :

La surface du parallélépipède crée par ces deux vecteurs est donc égale à 4.

Pour l’angle, on a trouvé que :

On applique donc :

Et il ne reste plus qu’à résoudre pour :

ou 30°

Et si on changeait l’ordre de multiplication des vecteurs ? En clair : et si on multipliait par ?

On trouve le même vecteur, de même norme – et donc de même surface – mais il va dans la direction inverse.

Et l’angle ?

ou 30°

L’angle, lui, n’a pas changé. On a eu chaud, parce que j’aurai eu du mal à expliquer pourquoi il serait différent selon qu’on le mesure dans un sens ou dans l’autre…

Le produit vectoriel n’est donc pas commutatif. La bonne nouvelle, c’est que si on change l’ordre du produit, le vecteur obtenu est le même mais dans l’autre direction :

Pour une simulation du calcul de l’angle et de la surface entre deux vecteurs, une appliquette Geogebra : surface et angle entre deux vecteurs.

Noter, en utilisant cette simulation, que l’angle calculé avec notre formule est toujours l’angle entre les deux vecteurs, quelle que soient leur coordonnées.