Matrice Jacobienne

On arrive très vite aux limites de ma compréhension de toutes choses mathématiques, mais persévérons un peu. De plus, ce qui suit est une opportunité d’utiliser ce fameux calcul de déterminant.

Notre objectif est d’exprimer un volume en coordonnées sphériques. Pour rappel, un volume élémentaire est donné par :

Ça semble simple : on exprime en fonction des coordonnées , et , on prend la dérivée et on multiplie… non ?

Non.

Tout simplement parce que, en exprimant en coordonnées sphériques, on a une fonction avec 3 variables.

Je n’ai pas beaucoup d’explications pour ce qui va suivre – je sais comment ça marche, mais pas vraiment pourquoi – mais procédons :

On appelle matrice Jacobienne une matrice des dérivées partielles de fonctions vectorielles.

Houlà. Y a des choses à déballer, là…

Une fonction vectorielle, c’est un vecteur où chaque dimension est une fonction. Par exemple, nous avons exprimé ce que vaut en coordonnées sphériques :

On ne dirait pas comme ça, mais ça représente trois fonctions :

Une dérivée partielle, c’est la dérivée par rapport à chacune des variables. Donc, les dérivées partielles de sont :

Et c’est quoi, en coordonnées sphériques ?

Chaque dimension contient trois dérivées partielles. Ça fait un total de neuf dérivées à trouver pour construire une matrice Jacobienne.

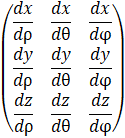
Hé bien autant s’y attaquer maintenant : chaque ligne de la matrice Jacobienne contient les dérivées partielles de chaque dimension. On trouve donc chaque dérivée partielle, et on la met dans la matrice.

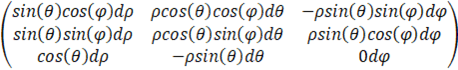
Ça m’a pris un moment, mais c’est fait. Place à la procédure :

On calcule le déterminant de cette matrice :

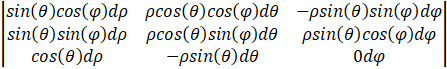
Pour la suite, je vais ne pas écrire , c’est bien assez compliqué comme ça…

On peut factoriser :

Et factoriser et à l’intérieur des parenthèses :

Comme , pas mal de choses s’annulent…

… et s’annulent encore.

Je réintègre et j’obtiens ce que je cherchais :

Intéressant. Il semble vraiment que le déterminant d’une matrice est lié à la surface ou au volume d’un objet décrit par cette matrice. On trouvera ça par des moyens détournés (regarder le dessin d’une sphère avec attention), mais c’est toujours intéressant de savoir qu’on peut trouver la même chose avec deux approches apparemment différentes.

Dans tous les cas, on a découvert une propriété : le déterminant d’une matrice Jacobienne est égal au volume. Je crois.

Essayons le même raisonnement avec les coordonnées cylindriques :

Je construis la matrice Jacobienne (trois dérivées pour chaque dimension) et j’en trouve le déterminant :

Ah c’était plus simple. On aurait dû commencer par là…

On a donc la définition d’un volume en coordonnées cylindriques :