Intégrales et théorème fondamental de l’analyse

Pour bien comprendre ce qui va suivre, je vais devoir prendre un exemple et essayer d’en tirer des généralités.

Prenons une fonction linéaire, passant par l’origine :

Supposons que je m’intéresse à la surface sous cette fonction. Je peux calculer la surface pour chaque élément : c’est simplement le produit de avec l’image de la fonction à cet endroit.

Je peux ensuite faire la somme de toutes ces surfaces…

… et créer une fonction avec ça. Ainsi, j’aurai une fonction pour la surface en fonction de .

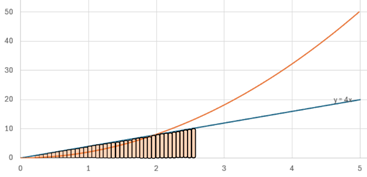Voilà qui est intéressant : la courbe obtenue est une fonction carrée qui passe par l’origine.

En utilisant les coordonnées de deux points par laquelle cette courbe passe, je peux calculer son coefficient directeur (voir le chapitre sur les fonctions simples) :

Pour et , .

La fonction représentant la surface est égale à .

Je dis ça, je dis rien, mais la primitive de , c’est justement . On dirait bien que la surface en dessous d’une courbe est liée aux primitives…

Une autre hypothèse, donc : la surface en dessous de la courbe est égale à la primitive évaluée entre deux limites (un intervalle entre deux valeurs pour ).

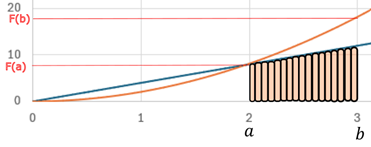Dis autrement : la surface sous la courbe entre deux points et est égale à la différence entre la primitive évaluée à et la primitive évaluée à .

Maintenant, comment avons-nous trouvé que c’était la surface ? On a simplement fait une somme de produits de avec . Si on allonge un peu la lettre S, on obtient l’intégrale, c’est-à-dire la somme de portions infiniment petites.

C’est le théorème fondamental de l’analyse et, dans un premier temps et comme on l’a vu, il permet de calculer la surface sous une courbe. Plus généralement, il permet de calculer n’importe quoi tant qu’on peut l’exprimer sous forme de fonction et le découper en petites parties – des distances, des surfaces, des volumes…

Comme pour les dérivées, on fait l’hypothèse que l’approximation nous permet de trouver la primitive de n’importe quelle fonction. Théoriquement.

Testons un peu cette hypothèse. Supposons une forme composée d’un triangle rectangle qui surmonte un rectangle. La largeur du rectangle est , et sa hauteur . La base du triangle est elle aussi et celle du triangle .

Avec un peu de géométrie, on trouve que la surface de cette forme est simplement :

Pour comparer, trouvons la fonction linéaire qui décrit l’hypoténuse du triangle. On connaît les coordonnées de deux points : et . On en déduit :

Sachant que l’intégrale entre deux points est la surface, on écrit :

On trouve la primitive de la fonction :

Appliquons le théorème fondamental de l’analyse :

On simplifie et on réorganise :

Ce qui est la même chose qu’on avait trouvé par géométrie.

Evidemment, utiliser une intégrale pour cet exemple est inutile – il est bien plus simple d’utiliser les formes géométriques de base. Mais pour d’autres cas, ce sera en fait bien utile.

Par exemple : la surface sous des courbes qui ne sont pas des lignes droites.

Simulations

Pour une simulation du calcul de la surface entre les racines d’un polynôme de degré 2, il y a une appliquette Geogebra : surface entre les racines d’un polynôme de degré 2.

Et pour une simulation du calcul de la surface entre deux polynômes de degré 2, il y aussi l’appliquette Geogebra : surface entre deux courbes.