Calculs de volumes cylindriques

On l’a vu, le volume d’un cylindre est simplement la surface de sa base multipliée par sa hauteur.

Et si cette hauteur était une fonction de ? Pour un cylindre normal, cette fonction est une constante, mais si c’était une fonction linéaire, ou carré, ou n’importe quelle fonction.

Ici, nous allons utiliser notre capacité à décrire une courbe avec une fonction, puis l’appliquer au concept d’intégrale – l’addition de petits morceaux, le théorème fondamental de l’analyse.

Prenons un cône. Sa base est .

Un cône peut être divisé en petits cylindres de hauteur . On en déduit la formule pour un petit volume :

Rappel : se dit dérivée de V et se dit dérivée de h. et sont des fonctions.

Maintenant, prenons l’apothème d’un cône. C’est une fonction linéaire qui va des coordonnées aux coordonnées (. On en déduit la fonction :

Pour calculer un élément de volume , nous avons besoin de la dérivée de . Trouvons là :

On intègre ce résultat à l’expression du volume :

Maintenant, nous pouvons prendre l’intégrale aux deux côtés de l’équation. A gauche, la variable d’intégration est le volume, donc on intègre de 0 à ; à droite, la variable d’intégration est , donc on intègre de 0 à .

Notez comme j’ai sorti les constantes qui multipliaient la variable d’intégration. La primitive en sera plus évidente.

Appliquons les limites d’intégration :

Tout cela se simplifie :

Ça ressemble en effet à la formule qu’une rapide recherche sur internet donne, mais pourquoi le signe négatif ?

C’est parce qu’on a commis une petite erreur sans grande importance : on a mal défini nos variables d’intégration du rayon. Et quand je dis sans grande importance, je mens.

Je disais qu’on additionnait des petits cylindres de hauteur . Mais au début, le cylindre a un rayon égal à . A la fin, il a un rayon de 0. Il faut donc d’inverser les variables d’intégration pour le rayon :

Lors de l’écriture de ce cours, j’ai presque volontairement commis cette erreur pour insister sur un point : il faut bien réfléchir avant de décider des variables d’intégration : où commence-t-on, où fini-t-on. Sinon, on se retrouve avec des résultats insensés qui prennent environ dix minutes à corriger alors qu’on doit préparer son prochain cours au lieu d’écrire des trucs que personne ne lit…

Le cours a été annulé, amusons-nous un peu : et si la fonction était une fonction carrée ?

Imaginons donc un cône dont l’apothème est défini par une fonction carrée. La hauteur de cette forme (le vertex) est , et le rayon de la base est .

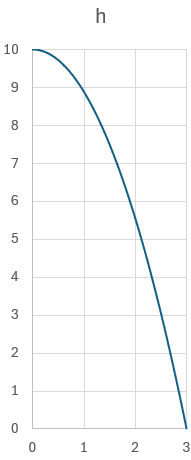On définit la fonction :

On trouve la dérivée et on l’intègre à la formule pour le volume d’un cylindre d’épaisseur :

Plus qu’à prendre l’intégrale (Je ne commets pas la même erreur que tout à l’heure) :

Et on simplifie.

On peut calculer manuellement (avec une feuille de calculs) la somme des volumes de petits cylindres de hauteur et comparer : ça marche.

Pour une simulation de ce précédent calcul, une appliquette Geogebra : volume sous une fonction carrée.