Stratégies de dérivation

On a développé tout ce qu’on sait des dérivées à partir d’une hypothèse : si je calcule la tangente entre deux points séparés par une distance , et que je fais en sorte que cet écart soit le plus petit possible (), puis que je fais de toutes ces valeurs une fonction, cette fonction est la dérivée.

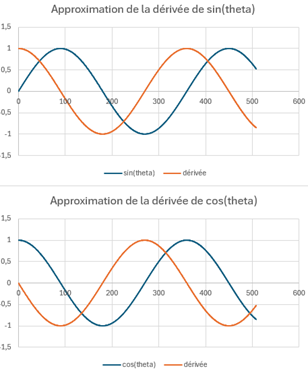En observant la dérivée que j’obtiens, j’en déduis pour les polynômes que :

Pour ,

Je peux appliquer la même procédure à n’importe quelle autre fonction.

Par exemple, la fonction . Si je calcule la dérivée (la tangente entre deux points) tout le long de la fonction, je trouve une autre fonction qui ressemble beaucoup à une fonction .

J’en conclus :

Pour ,

Je fais le test avec , et j’obtiens quelque chose qui ressemble beaucoup à .

J’en conclus :

Pour ,

On peut deviner (et on pourra vérifier par soi-même) que la dérivée de est , et celle de est .

J’en profite pour noter que si la dérivée de , c’est , alors la primitive de , c’est .

Pour la fonction , je rencontre des difficultés : non seulement je n’arrive pas à obtenir un graphique lisible sur une large gamme de valeurs, mais quand je zoome assez fort sur le graphique, je n’ai aucune idée de ce que je regarde. On verra ça plus tard.

On notera par ailleurs, après avoir fait le test, que :

Pour , la dérivée est

Pour , la dérivée est

Eh oui : la fonction exponentielle est égale à sa propre dérivée. Pour l’anecdote, c’est en connaissant cette propriété et en faisant des approximations que j’ai trouvé la valeur de : 2,71828…

Il y a des cas hélas où trouver la dérivée n’est pas simple. Et là encore, sans pouvoir le prouver, je donne les trois règles à mémoriser pour des cas particuliers :

Dérivée d’un produit de fonctions

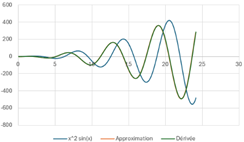Pour le produit de fonctions , la dérivée est

Imaginons une fonction . Selon cette règle, la dérivée serait :

J’ai fait le test en comparant l’approximation avec ce résultat, et ça marche : si vous ne voyez pas la courbe rouge de l’approximation dans le graphique ci-contre, c’est qu’elle pile en dessous de la celle pour la dérivée…

Dérivée d’un quotient de fonctions

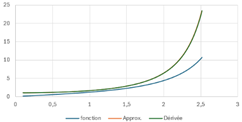Pour le quotient de fonction , la dérivée est

Imaginons une fonction . Selon cette règle, la dérivée serait :

J’ai vérifié encore avec une approximation, et là encore, ça a l’air de bien marcher, cette petite règle absolument pas compliquée…

Je pourrais peut être en profiter pour savoir ce que c’est, la dérivée de . Parce qu’on se souvient que :

Allons-y :

On utilise l’identité trigonométrique :

Le résultat se réécrit :

Pas étonnant que je ne pouvais pas la deviner, celle-là…

Fonctions imbriquées

Pour , la dérivée est

C’est probablement la plus importante des trois : lorsqu’une fonction contient elle-même une fonction. On prend la dérivée de la fonction , et on la multiplie par la dérivée de la fonction . Ce qui est à l’intérieur de la fonction est inchangé.

Par exemple : – une fonction dans une fonction sinus. On applique :

Logiciels de calcul formel

Je ne connais pas d’autres règles de dérivation – il me semble qu’avec tout ça on peut s’occuper de pas mal de problèmes – mais il en existe. Parfois, les choses deviennent trop compliquées, et la technologie peut nous venir en aide.

On a déjà vu qu’on peut toujours faire une approximation de la dérivée d’une fonction. Trouver la fonction qui épouse parfaitement cette approximation peut s’avérer difficile, toutefois.

Un logiciel de calcul formel peut théoriquement résoudre n’importe quelle opération, y compris des opérations contenant des lettres, y compris des équations, des dérivées, des intégrales… Deux problèmes toutefois :

· parfois, il est très difficile de comprendre la réponse du logiciel. Cela demande donc de tester la réponse en la comparant à une approximation.

· le langage utilisé par le logiciel doit être appris. Wolfram Alpha, une version en ligne du logiciel de référence Mathematica, demande des formules en Latex ; Geogebra, libre, gratuit et utilisable en ligne, a son propre codage en français.

Il faudra donc faire un peu de recherche avant de pouvoir utiliser ces logiciels de calculs formels.