Systèmes de coordonnées et intégrales en trois dimensions

Nous avons les intégrales, nous avons les définitions des surfaces et volumes : calculons des trucs !

Dans un espace en trois dimensions, un système de coordonnée est un système qui utilise trois axes perpendiculaires les uns aux autres pour décrire la position d’un point.

Une surface est le produit de deux dimensions ; par exemple, pour une surface dans et  :

Un volume est le produit de trois dimensions :

Vous l’avez compris : nous allons utiliser le concept d’intégrales pour calculer des surfaces et des volumes décrits par des fonctions.

Dans le système cartésien que vous connaissez bien, les axes sont des lignes droites : , et .

Si nous voulons calculer la surface d’un carré de côté , on définit les limites :

On applique la définition de la surface :

Ce que vous découvrez ici sous vos yeux ébahis, c’est une double intégrale, ou une intégrale de surface. En effet, il y a deux variables d’intégration ( et ), donc il faut deux intégrales.

On commence toujours par l’intégrale à l’intérieur, puis on résout la suivante, et ainsi de suite en allant jusqu’à l’extérieur.

Ça semble beaucoup de travail pour trouver la surface d’un carré.

Supposons maintenant que la limite supérieure dans le sens de soit une fonction de  : .

Noter que, comme j’ai une fonction de dans une limite, je commence par celle-là avant de prendre l’intégrale sur . L’idée est de prendre en compte les variables qui se trouvent dans la fonction.

Bien. On a retrouvé l’intégrale pour calculer la surface en dessous d’une courbe. Ça avance vite, hein ?

OK. Je suppose que si je faisais la même chose pour un volume, je retrouverais la formule pour calculer le volume d’un cube. Passons cela.

Et si le volume du cube était limité dans le sens de par une fonction ?

Encore une fois : est la dimension dans laquelle s’applique. On fait en sorte de commencer par cette intégrale.

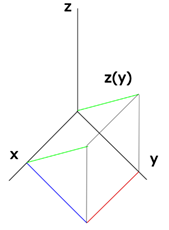Bon, ça demande d’être visualisé, tout ça.

Supposons un coin – un pavé droit coupé en deux dans le sens de la diagonale. Dans le sens de et , la distance entre l’axe et le bord du coin est constante. Dans le sens de , elle est donnée par .

On écrit l’intégrale :

On commence par l’intégrale centrale.

Oui, je commence à prendre des raccourcis, mais à ce stade, si vous ne comprenez pas comment je suis passé de la première étape à la deuxième, ça veut dire qu’il faut que vous preniez un peu de recul. Par là, je veux dire retourner en arrière. Et revenir ici.

C’est bon, vous êtes revenus ?

Du point de vue de , est une constante. L’intégrale suivante est donc simple :

Et enfin, l’intégrale évaluée sur :

Vérifions ce résultat avec un peu de géométrie.

Si , alors la hauteur à est égale à .

Le volume du cube est donc .

Et comme un coin, c’est un cube coupé en deux :

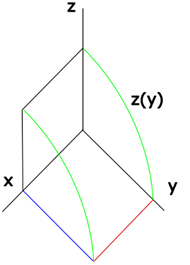On pourrait s’amuser un peu, et se poser la question : et si la fonction était une fonction carrée dont l’extremum est à et dont la racine est à .

D’abord, la fonction :

On connaît l’ordonnée à l’origine – c’est – donc plus qu’à trouver le coefficient directeur.

J’ai coloré le coefficient directeur pour le différencier de la longueur .

On a trouvé la fonction :

Maintenant, on met l’intégrale en place :

Et, intégrale par intégrale, on se rapproche de la réponse :

C’est frustrant : je ne sais pas si j’ai raison. Mais je ne vois aucun problème dans ce raisonnement et dans ce résultat – la distance est au cube, ce à quoi on s’attend avec un volume. Je m’attendais juste à ce que le résultat soit un peu moins… joli. On va dire que je suis confiant à 70%...

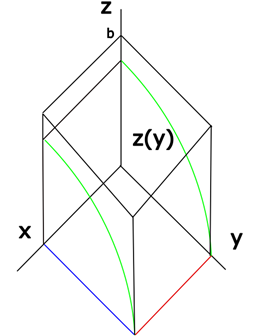Allez, ça m’embête un peu. Donc, élaborons une stratégie. On pourrait calculer un volume qui irait de la fonction jusqu’à une certaine distance . L’intégrale deviendrait :

Le volume entier est celui d’un bloc de base et de hauteur .

Et en utilisant les volumes des deux formes qu’on a calculé :

On dirait que j’ai raison. Mon syndrome de l’imposteur est toujours présent, mais ma confiance dans ce résultat a monté à 80%.