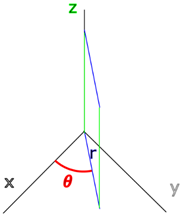
Coordonnées cylindriques

Je sais que ce n’est pas évident, mais un angle est perpendiculaire à la droite d’où il part.

Il faudrait que je dessine ça.

Ca y est, c’est dessiné. Observez que l’axe est perpendiculaire à , mais aussi à . Car ce sont les trois coordonnées cylindriques : .

Si on veut convertir des coordonnées cartésiennes en coordonnées cylindriques, un peu de trigonométrie et de Pythagore suffisent :

Mais ce n’est pas ça qui nous intéresse. Ce qui nous intéresse, c’est de calculer des surfaces et des volumes.

Commençons par une surface plane, uniquement et . Incidemment, on appelle ça les coordonnées polaires, contenant les deux premières dimensions des coordonnées cylindriques.

Nous devons donc traduire la définition de la surface en coordonnées cartésiennes :

… en coordonnées cylindriques.

Bon. On a utilisé les matrices Jacobiennes pour définir des éléments de volumes en coordonnées cylindriques et sphériques. Par géométrie, on peut aussi les définir :

· qu’une surface est le produit de deux dimensions (en mètres)

· que la longueur d’un arc de cercle est donnée par , où est constant – donc un élément infiniment petit de distance dans cette direction est

Ainsi, les deux éléments de longueur sont et . Et un élément de surface en coordonnées polaires est :

Vérifions en calculant la surface d’un disque ; les limites d’intégrations sont 0 à dans le sens de et de 0 à dans le sens de  :

Très bien, ça a l’air de marcher. Maintenant, imaginons une surface un peu plus complexe. Par exemple, si le rayon était une fonction de l’angle. C’est-à-dire qu’il serait à zéro quand l’angle est à zéro, et à quand l’angle est à , et qu’entre les deux, il augmenterait linéairement en fonction de l’angle.

La fonction qui décrirait ça serait . A , . A , .

On place ça dans l’intégrale, et on intègre.

Encore une fois, la fonction pour contient la variable , c’est donc d’elle que je dois m’occuper en premier.

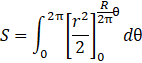
Pour vérifier que je ne me trompe pas, rien ne vaut Wikipedia : la spirale d’Archimède est donnée par la fonction et la surface balayée par le rayon au fur et à mesure qu’il tourne est égale à .

Dans mon exemple, . Selon Archimède, donc :

Encore une fois, tout seul comme un grand, j’ai trouvé quelque chose de correct. Toujours le syndrome de l’imposteur, mais encore un peu plus de confiance dans ce que je dis.

Attention toutefois : cette procédure ne vaut que pour des angles inférieurs à . Au-delà, la procédure compterait des éléments de surface plusieurs fois. L’intégrale compte la surface balayée par le rayon, et si on tourne plusieurs fois autour d’un axe, on balaye plusieurs fois la même surface.

Fort de ce succès, et si on calculait le volume d’un cône ? On l’a déjà fait par des moyens détournés, mais ce serait bien de le confirmer.

En coordonnées cylindriques, un élément de volume est :

Oui, c’est simplement la surface de la base multipliée par la hauteur.

La hauteur d’un cône varie avec le rayon. On écrit donc la fonction :

Les limites d’intégration sont donc :

Pour la première intégrale, est une constante. On intègre sur  :

On distribue, on intègre sur , et on simplifie :

Et on intègre sur :

On avait déjà trouvé ce résultat par des moyens détournés (l’addition de disques de hauteur ). Cette méthode est plus qu’une confirmation : c’est une généralisation.

Bien. Et si c’était la surface du cône qu’on voulait calculer ?

Dans ce cas, on n’intègrerait pas sur . Mais serait toujours fonction de .

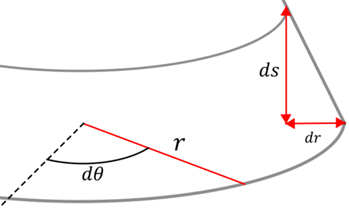On peut déterminer les dimensions d’un élément de surface : le produit de la distance dans le sens de avec celui dans le sens de l’apothème du cône. Et l’apothème du cône, c’est Pythagore qui nous la donne.

Maintenant, qu’est-ce que c’est, ? C’est la dérivée de , qu’on vient juste d’exprimer en fonction de ; prenons donc la dérivée de par rapport à :

On peut réécrire notre élément de surface :

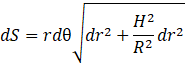
Factorisons le :

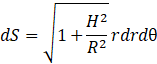
Maintenant, on peut intégrer. Dans le sens de , les limites d’intégration sont de zéro à ; dans le sens de , de zéro à .

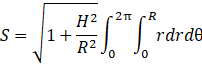
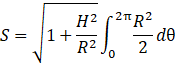
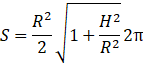
Tout cela se simplifie gentiment :

Et comme , c’est l’apothème du cône :

On avait déjà trouvé ce résultat en utilisant quelques relations en géométrie : c’est rassurant qu’une seconde méthode donne la même chose. En fait, en regardant de plus près, on s’apercevrait que ces deux méthodes sont en fait identiques, mais passons…