Coordonnées sphériques

Les coordonnées sphériques sont en fait celles qu’on utilise en géographie :

· le rayon correspond à l’altitude, plus le rayon de la Terre

· l’angle correspond à la longitude

· l’angle correspond à la latitude

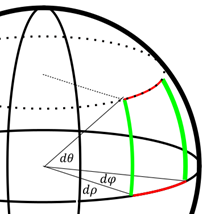
Comme avec les coordonnées sphériques, on doit trouver des expressions avec des distances pour pouvoir calculer des surfaces et des volumes.

Tout d’abord, dans le sens de , on a…

Ensuite dans le sens d’une longitude, on a

Enfin, dans le sens d’une latitude, on a

Donc, un élément de volume en coordonnées sphériques est donné par :

Trouvons tout de suite la formule pour le volume d’une sphère, ça va me permettre de justifier les limites dans chaque dimension :

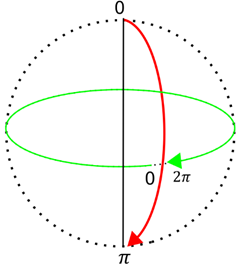Dans le sens de , on va très logiquement de zéro à .

Dans le sens de , on fait un tour complet : .

Dans le sens de , on ne parcourt qu’un demi-cercle ; sinon, on balayerait deux fois une surface et on la compterait deux fois. On parcourt donc

Résolvons les intégrales :

Qui est en effet, selon tous les vrais bouquins de mathématiques, la formule pour le volume d’une sphère.

Pour la surface d’une sphère, on a les mêmes dimensions mais on n’intègre pas sur – c’est constant.

Maintenant, armé de tout cela, on pourrait calculer le volume d’objets rigolos, comme celui d’un œuf. Mais cela dépasse l’objet de ce document.