Second degré

Une équation différentielle homogène du second ordre est une équation qui contient une fonction et sa dérivée seconde.

La seconde dérivée d’une fonction par rapport à une variable s’écrira ici ou plus concisément .

Donc, la forme typique d’une équation différentielle du second ordre est :

Ou, plus concisément :

La procédure de résolution, sans plus d’explications, est un peu longue.

D’abord, on remplace les fonctions et leurs dérivées par une variable à une puissance égale au degré (nombre de dérivée).

On se retrouve alors avec une équation du second degré avec comme inconnue : l’équation caractéristique.

Les solutions de cette équation sont données par la formule quadratique :

La solution de l’équation différentielle est enfin la somme de deux fonctions qui rappellent la solution d’une équation différentielle du premier ordre :

où et sont des constantes déterminées par des conditions initiales.

Bon. Je pense que c’est assez compliqué pour diviser les équations différentielles homogènes du second ordre en deux parties : le cas où il n’y pas de terme , et le cas où il y en a un.

Ah, et aussi : est négatif. Je garde les complications pour plus tard. L’équation caractéristique est :

On trouve :

La solution est donc :

Très bien. Facile. Bon.

Maintenant, et si était positif ?

Oh. Problème. On a la racine carrée d’un nombre négatif. Et ça, c’est incalculable. La racine carrée est la réciproque de l’exposant 2, et n’importe quel nombre à l’exposant 2 donne un nombre positif. Pas un nombre négatif…

Bon. On va devoir tricher. Et par tricher, je veux dire résumer plusieurs siècles de travail de mathématiciens qui ont donné leur nom à des théorèmes comme à des avenues en une lettre : .

Le nombre est un nombre imaginaire. Sa seule et unique propriété se découvre quand on le met au carré :

Avec dans notre arsenal, on peut réécrire notre résultat :

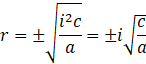
On peut donc écrire notre solution :

On est bien avancés, hein ?

Bon. On va avoir besoin de la relation de Euler.

Je ne sais pas pourquoi (une histoire de séries de Taylor), mais la relation de Euler dit ceci :

En voyant cette relation, il me vient une idée : et si je remplaçais par ?

Et ça, ça me garde éveillé la nuit.

Le nombre est irrationnel ; est lui aussi irrationnel. Mais dans cette opération, ces deux nombres ensemble donnent un nombre exact. Personnellement, je trouve que cela confère des pouvoirs magiques à ce fameux nombre . Qui pourtant, à la surface, n’a pour seule propriété que son carré est égal à -1.

Passons avec regret.

Et utilisons la relation de Euler pour voir si elle peut nous tirer d’embarras.

On développe, et on factorise :

Il y a deux termes entre parenthèses qui sont des constantes. Appelons-les :

Et réécrivons notre solution :

Je suis un peu embêté par ce , parce qu’il contient cette lettre effrayante, . Mais je vais faire de mon mieux pour l’oublier car, après tout, ce n’est qu’une constante…

Il ne resterait plus à ce stade qu’à appliquer les conditions initiales. Je pense qu’il serait bon de plutôt présenter un exemple. En physique.

Je dispose un ressort à l’horizontale sur une table, et je l’attache à un point. J’attache à l’autre bout une masse, et je tire sur le ressort. Lorsque je le relâche, la masse oscille entre la gauche et la droite.

Très bien. La force avec laquelle le ressort retient la masse est donnée par la loi de Hooke :

où est le coefficient de raideur du ressort.

Au moment où je relâche le ressort, la situation est dynamique. Dans ce cas, la somme des forces en présence est égale à , où est l’accélération. La seule force en présence étant , j’écris :

L’accélération est la seconde dérivée de la position . Je réécris donc mon équation sous la forme d’une équation différentielle :

L’équation caractéristique donne :

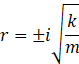
Et la solution de l’équation différentielle :

Qui, selon la relation de Euler, se réécrit :

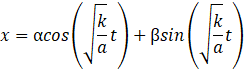
Maintenant, appliquons les conditions initiales :

A , on relâche le ressort. Ça veut dire qu’à ce moment précis, on l’a étiré sur une distance . La position à est donc :

Fort bien. Maintenant, qu’en est-il de la vitesse ? A , elle est égale à zéro : le ressort ne s’est pas encore contracté, il n’a pas encore commencé son mouvement. On trouve donc la dérivée de la position – à propos, la dérivée de la position sur le temps , c’est la définition de la vitesse :

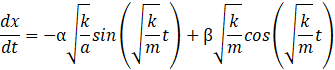
Et, comme on l’a dit, tout ça est égal à 0 lorsque :

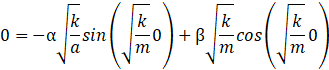
Cette expression qui, il faut bien le dire, fait un peu mal aux yeux, se simplifie dramatiquement :

On peut donc réécrire notre solution :

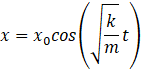
C’est l’équation de mouvement d’un oscillateur. Le terme qui multiplie dans le cosinus est nécessairement la vitesse angulaire (l’argument d’une fonction trigonométrique étant toujours un angle en radians), c’est-à-dire l’angle parcouru chaque seconde :

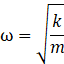
Mais un ressort, me direz-vous, ça ne parcourt pas un angle. Ca va et vient et puis c’est tout, non ? Non ?

C’est vrai, rassurez-vous. Calmez-vous, tout va bien se passer.

Il s’agit ici d’une représentation mathématique d’un phénomène physique. Bien sûr que le ressort ne se met pas à tourner, mais son mouvement peut être représenté par une fonction trigonométrique. Et le point même de la physique est de représenter le monde en utilisant les outils mathématiques qu’on a développé pour mieux le comprendre.