Nous avons vu dans l’épisode précédent comment résoudre une équation différentielle du second ordre homogène lorsqu’il n’y a pas de première dérivée.

Il va bien falloir maintenant se coltiner le cas où il y en a un :

L’équation caractéristique donne :

Les solutions de cette équation sont données par la formule quadratique :

Mais là, je dis stop. Les choses deviennent trop compliquées. Pour ne pas s’y perdre, je vais tout d’abord séparer les solutions :

Et mes solutions sont :

Donc, la solution de l’équation différentielle est :

Ca va nous permettre de nous concentrer sur ce qui se passe entre les parenthèses et de laisser intact ce qui est à l’extérieur.

Pour ce qui est entre les parenthèses, il y a trois possibilités.

La première est la plus simple : est positif. La solution reste telle quelle.

La seconde est encore plus simple : est égal à zéro. Alors la solution de l’équation différentielle devient alors simplement :

C’est quand devient négatif que les choses se compliquent. Et que cet hideux repointe le bout de son nez visqueux.

Là, il est nécessaire de faire une opération pour le faire apparaître :

J’ai multiplié l’intérieur de la racine carré par moins un deux fois : rien n’est changé.

Je sais qu’un de ces est en fait incognito. Je le sors de la racine, et je distribue l’autre .

Et la solution de l’équation différentielle se trouve être :

On comprend que ça fait une fonction qui fait un peu mal aux yeux.

Passons donc directement à l’exemple.

En reprenant notre exemple de tout à l’heure, en fait, et en y introduisant un amortissement . Pour ceux qui n’ont pas suivi : l’exemple du ressort qui oscille.

Tout de suite, et parce que je sais que plus tard, ça simplifiera les écritures, je définis deux constantes :

L’équation différentielle devient alors un peu plus lisible:

On trouve l’équation caractéristique :

Et on trouve les solutions :

Maintenant, décrivons les trois cas :

· si , alors la solution est

où

· si , alors la solution est :

On parle alors de régime critique.

· si , alors la solution est :

où

Pour cette dernière solution, il y a encore une étape pour se débarrasser des  : la relation de Euler.

Bien. Comme d’habitude, la procédure demande de la rigueur mais, tant qu’on fait bien attention, les procédures sont assez simples à suivre.

Mais on n’a pas fini.

Eh oui, nous n’avons pas défini de conditions initiales.

Reprenons donc.

Au début de l’oscillation, . Et à ce même moment, . Autrement dit : .

Commençons par le cas le plus simple :

Facile :

Donc :

Ensuite, le cas où :

Prenons maintenant la dérivée de ce truc, ça devrait prendre une minute…

Bien, ça demande un peu de concentration. Appliquons donc cette seconde condition initiale :

Merci à celui qui a inventé copier-coller.

Tout cela se simplifie :

Comme et, logiquement, :

Et donc la solution est :

Par miracle, ça a l’air de marcher. A , tout se simplifie en .

Enfin, le cas où .

OK, c’était facile. Et maintenant, on doit prendre la dérivée de cette monstruosité.

Là, on a utilisé deux des règles de dérivation qu’on a vues il y a longtemps. Plus qu’à remplacer tous ces par des zéros…

Et comme on a vu que , on peut résoudre pour et obtenir une jolie expression :

On met toutes ces informations dans la solution :

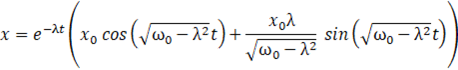
Je voudrais vous rappeler à ce point que nous cherchons à représenter mathématiquement le mouvement d’un ressort… Ca vaudrait le coup de tout compiler avec du vocabulaire de physique :

Régime apériodique (pas de rebonds) :

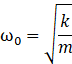
Régime pseudopériodique (rebonds) :

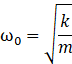
D’accord. Ça ressemble au truc le plus long et le plus compliqué qu’on ait jamais fait. Mais quand on y pense, chaque étape prise indépendamment était relativement simple. Mais c’est la taille du résultat et les pages d’écritures qui impressionne.

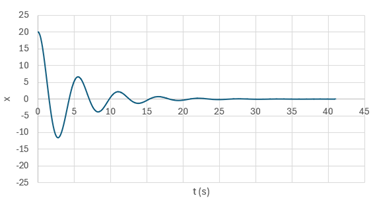
Reste qu’il faut tester ça. En simulant tout ça dans une feuille de calculs…

Après de multiples fautes de frappe : ça marche. Ou en tous cas, la fonction décrivant le mouvement du ressort en fonction de l’amortissement semble s’accorder à ce qui se produit dans la réalité.

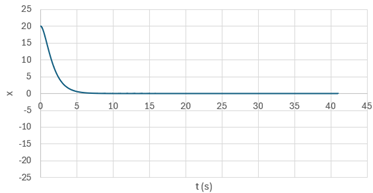En dessous d’un certain ammortissement, l’oscillateur oscille un peu avant de revenir à son état de repos.

Au dessus d’un certain ammortissement, il n’y a aucune oscillation : le ressort revient à sa position de repos.