Décomposition

Calculer la surface d’un objet plan revient à le décomposer en formes simples : des rectangles, des triangles, des arcs de disques, etc. Commençons avec un exemple simple : le triangle commun.

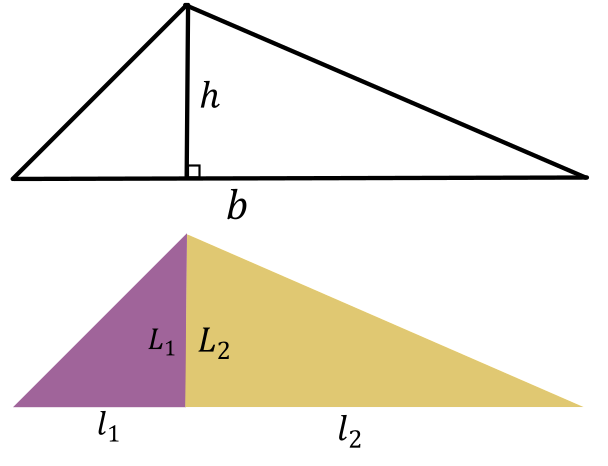
Un triangle a une base \(b\) et une hauteur \(h\). Il peut être décomposé en deux triangles rectangles (avec un angle droit), respectivement de largeur \(l_{1}\) et \(l_{2}\), et de longueur \(L_{1}\) et \(L_{2}\).

Tout de suite, on constate que :

\[L_{1} = L_{2} = h\]

Les surfaces des deux triangles sont respectivement, comme vu précédemment :

\[S_{1} = \frac{l_{1} \times h}{2}\]

\[S_{2} = \frac{l_{2} \times h}{2}\]

La surface du triangle complet est simplement la somme des deux surfaces :

\[S = S_{1} + S_{2}\]

\[S\ = \ \frac{l_{1} \times h}{2} + \frac{l_{2} \times h}{2}\]

On peut factoriser :

\[S = \frac{h}{2}\left( l_{1} + l_{2} \right)\]

Sachant que la base \(b\) est simplement la somme des deux largeurs :

\[S=\frac{b \times h}{2}\]

On devine alors que la surface d’un triangle, quel qu’il soit, est toujours donnée par la même formule (base fois hauteur divisée par deux). Et c’est le cas.

Prenons un autre exemple : la surface d’un cône.

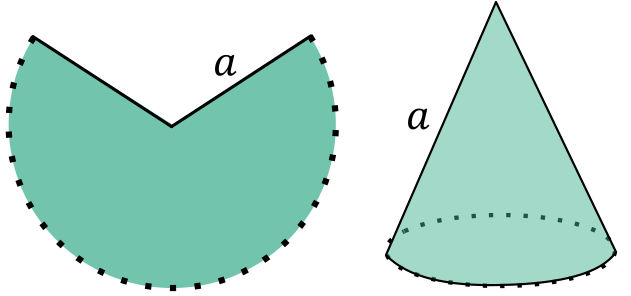Un cône aplati est simplement le secteur d’un disque dont le rayon est égal à l’apothème du cône – et l’apothème \(a\) est l’hypoténuse d’un triangle de base \(R\) et de hauteur \(H\). L’arc de cercle est égal au périmètre de la base.

Très bien. Exprimons tout cela avec des équations.

D’abord, on se rappelle de comment calculer la surface d’un secteur :

\[S = \frac{\theta}{2}a^{2}\]

Ensuite, l’apothème du cône (par Pythagore) :

\[a = \sqrt{R^{2} + H^{2}}\]

Et enfin, l’égalité entre l’arc de cercle et le périmètre :

\[\theta a\ = \ 2\pi R\]

Qu’on peut résoudre directement pour \(\text{θ~}\):

\[\theta = \frac{2\pi R}{a}\]

Tout d’abord, dans la première expression, remplaçons \(\text{θ~}\)à l’aide de la dernière expression :

\[S = \frac{2\pi R}{2a}a^{2}\]

\[S\ = \pi R\ a\]

Ensuite, remplaçons \(a\ \):

\[S = \pi R\sqrt{R^{2} + H^{2}}\]

Ou

\[S\ = \ \pi R\ a\]

Et voilà.

Nous reviendrons sur cette preuve lorsque nous parlerons des intégrales de surface et de volume mais déjà, avec quelques outils simples, on peut trouver des quantités intéressantes.