Les fonctions sinus et cosinus sont des fonctions trigonométriques décrivant l'évolution des distances au fur et à mesure qu'on se déplace sur le périmètre d'un cercle. Dans l'animation ci-dessous, on fait évoluer l'angle pour deux fonctions trigonométriques:
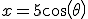
x = 5 cos(\theta)
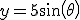
y = 5 sin(\theta)
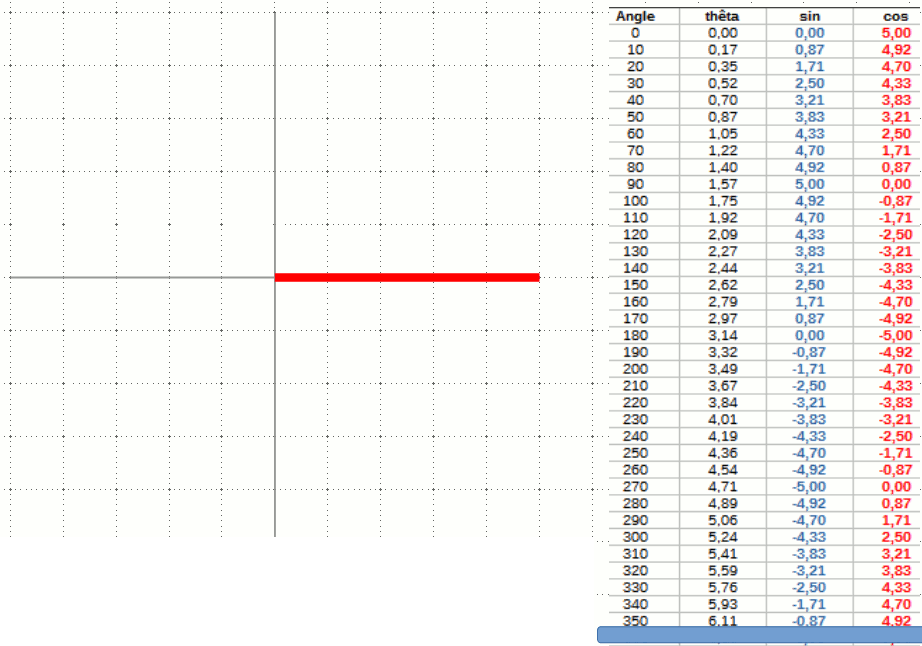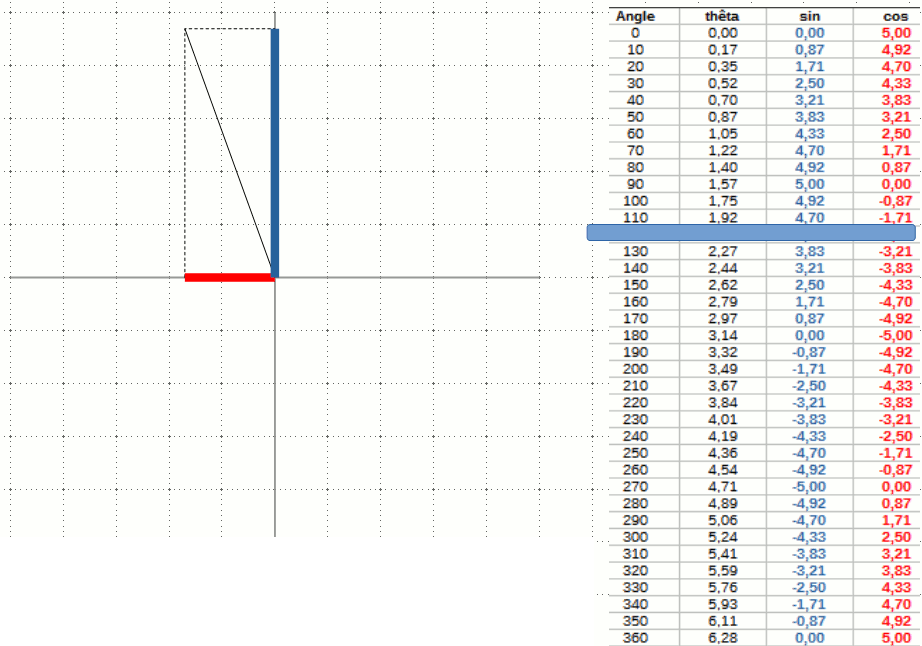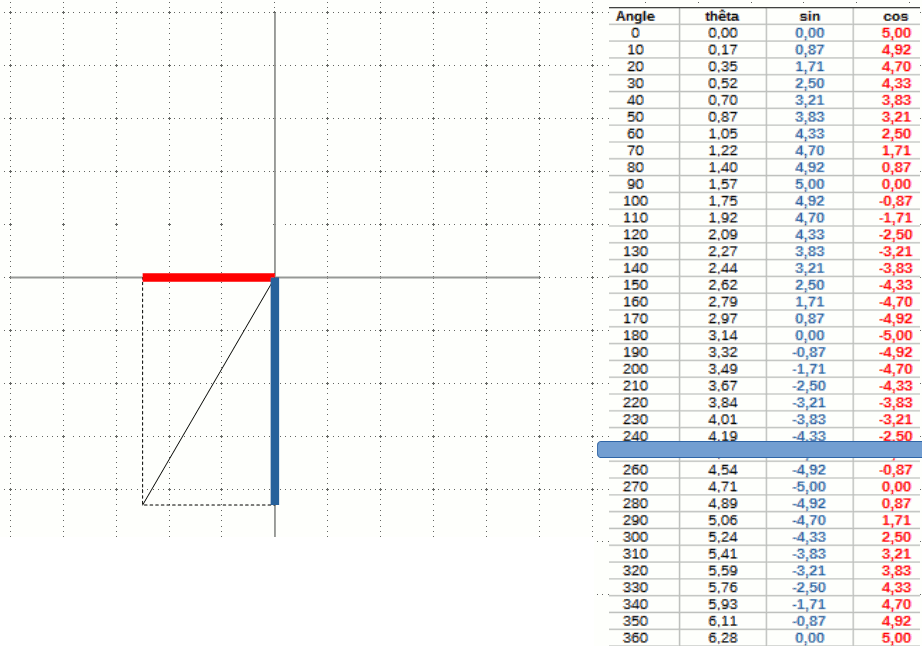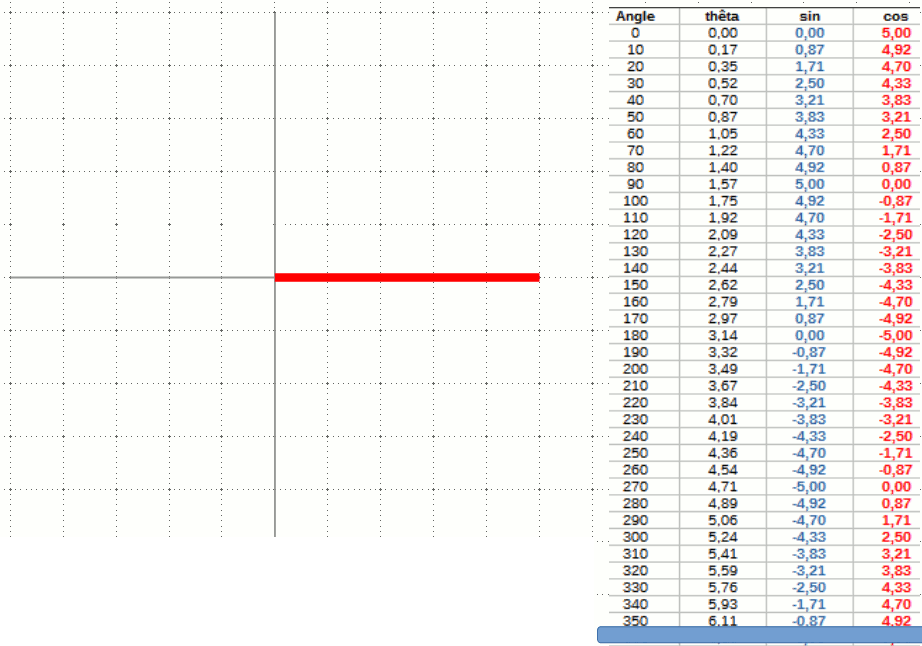
On remarque que la première formule donne la base x d'un triangle rectangle dont l'hypoténuse est égale au rayon du cercle. La deuxième formule, elle, donne sa hauteur y. Tout ce dont on a besoin est le rayon du cercle - l'hypoténuse - et l'angle.
 On peut donc utiliser ces fonctions trigonométriques pour trouver une dimension d'un triangle rectangle à partir de la valeur d'un de ses angles et d'un de ses côtés.
On peut donc utiliser ces fonctions trigonométriques pour trouver une dimension d'un triangle rectangle à partir de la valeur d'un de ses angles et d'un de ses côtés.
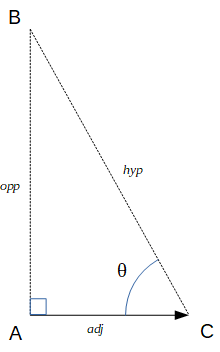
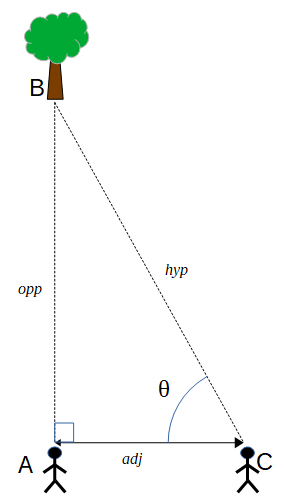
On définit d'abord les côtés du triangle:
- l'hypoténuse, son côté le plus long (le rayon du cercle dans l'expérience précédente)
- l'adjacente, le côté à côté de l'angle d'intérêt
- l'opposée, le côté faisant face à l'angle d'intérêt
On définit ensuite en ces termes les fonctions trigonométriques:
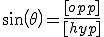
sin(\theta)= \frac{[opp]}{[hyp]}
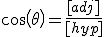
cos(\theta)=\frac{[adj]}{[hyp]}
- On peut en créer une troisième, la tangente:
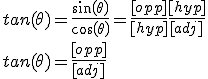
tan(\theta) = \frac{sin(\theta)}{cos(\theta)} = \frac{[opp]}{[hyp]} \frac{[hyp]}{[adj]}\\ tan(\theta)=\frac{[opp]}{[adj]}
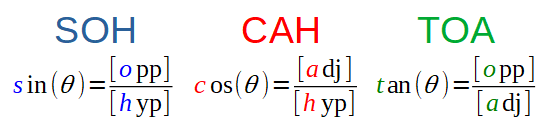 Il existe un moyen mnémotechnique pour se rappeler de ces trois fonctions trigonométriques: SOH CAH TOA, décrit dans l'illustration ci-contre.
Il existe un moyen mnémotechnique pour se rappeler de ces trois fonctions trigonométriques: SOH CAH TOA, décrit dans l'illustration ci-contre.
Parfois, c'est l'angle qu'on recherche. Il faut alors savoir que l'inverse d'une fonction trigonométrique est indiquée par les fonctions ASIN, ACOS et ATAN (tableur) ou les touches sin-1, cos-1 et tan-1 (calculatrice).
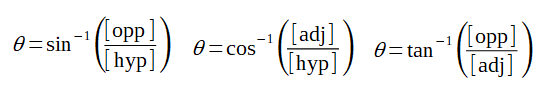

 On peut donc utiliser ces fonctions trigonométriques pour trouver une dimension d'un triangle rectangle à partir de la valeur d'un de ses angles et d'un de ses côtés.
On peut donc utiliser ces fonctions trigonométriques pour trouver une dimension d'un triangle rectangle à partir de la valeur d'un de ses angles et d'un de ses côtés.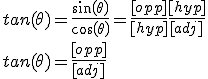
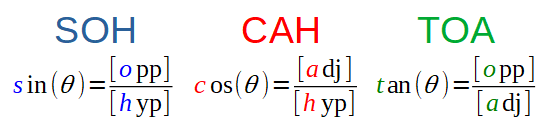 Il existe un moyen mnémotechnique pour se rappeler de ces trois fonctions trigonométriques: SOH CAH TOA, décrit dans l'illustration ci-contre.
Il existe un moyen mnémotechnique pour se rappeler de ces trois fonctions trigonométriques: SOH CAH TOA, décrit dans l'illustration ci-contre.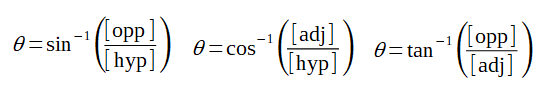
 On sait maintenant que pour mesurer une distance dans un triangle rectangle, on n'a besoin que d'un angle, d'une de ses dimensions et d'une fonction trigonométrique.
On sait maintenant que pour mesurer une distance dans un triangle rectangle, on n'a besoin que d'un angle, d'une de ses dimensions et d'une fonction trigonométrique.