Le diagramme de Venn est un moyen simple et intuitif de calculer des probabilités pour un petit nombre d’univers. Après avoir calculé les probabilités, on inscrit dans ce diagramme le nombre de fois qu’un événement arrive lorsqu’on répète une expérience autant de fois que son univers.
Dans l’expérience ci-après, nous allons utiliser un jeu de trois dés ayant un nombre de faces différents pour illustrer son utilisation.
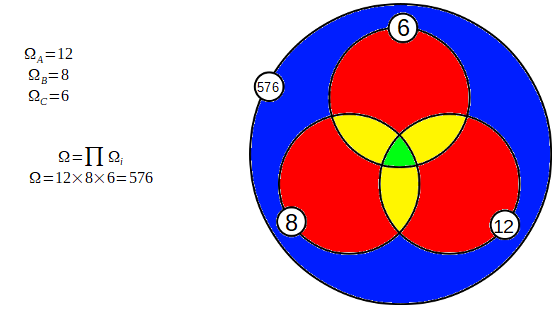
Nous avons un dé à 12 faces, un dé à 8 faces et un dé à 6 faces. L’univers de chacun de ces dés est le nombre de faces qu’il a.
La première chose à faire est de calculer l’univers entier de cette expérience. Cela nous donnera le nombre total de combinaisons possibles.
On sait que l’univers entier est le produit de tous les univers en présence. L’univers de cette expérience est donc égal à 576.
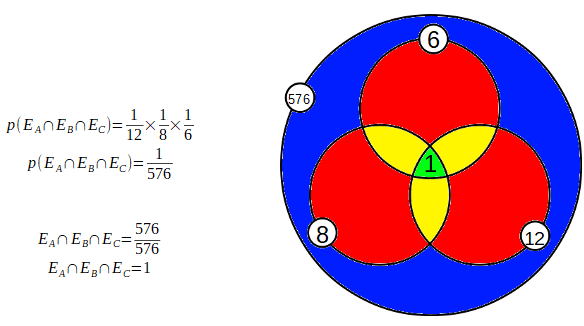
Choisissons un événement pour chacun de ces dés :
-
EA : le dé à 12 faces sort un 6
-
EB : le dé à 8 faces sort un 6
-
EC : le dé à 6 faces sort un 6
On sait que tous ces événements sont compatibles.