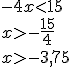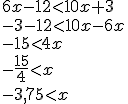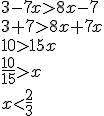Si une équation dit que ce qui est à gauche est égal à ce qui est à droite, une inéquation dit ce qui est à gauche est plus ou moins grand que à ce qui est à droite.

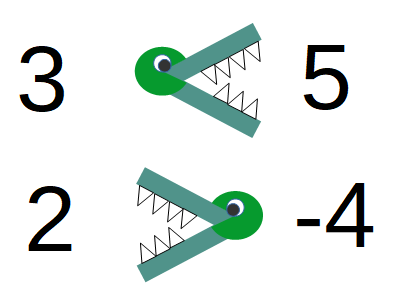Une inéquation est donc la même chose qu'une équation, sauf qu'on utilise les signes < et > à la place du signe =. Pour mémoire, la signification de ces symboles est bien expliquée par l'analogie du crocodile : le crocodile mange toujours le nombre le plus grand. Le signe < veut donc dire "ce qui est à gauche est moins grand que ce qui est à droite"; le signe > veut dire "ce qui est à droite est moins grand que ce qui est à gauche".

Prenons par exemple l'exemple suivant:

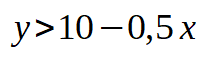
Cette inéquation nous dit que toutes les valeurs de y sont plus grandes que toutes les valeurs données par l'expression à droite du signe.

Par exemple, si x est égal à 5 :

La valeur de y est donc supérieure à 7,5.

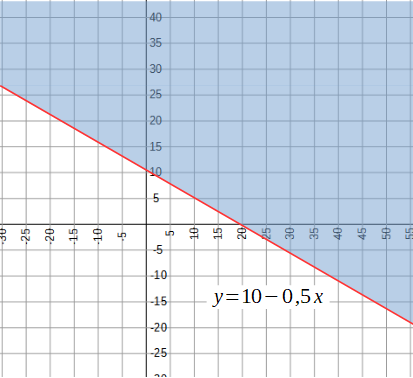
Graphiquement, toutes les valeurs au-dessus de la ligne représentant l'équation sont des valeurs acceptables de y. Dans l'illustration ci-contre, cela correspond à la zone bleue.

Par exemple, si x est égal à 20, toutes les valeurs au dessus de 0 sont des valeurs possibles pour y. Par ailleurs, si y est supérieur à 10, alors toutes les valeurs au dessus de 0 sont des valeurs possibles pour x.

Par contre, si x est égal à 10, alors -10 n'est pas une valeur possible pour y. Et si y est égal à 10, alors -5 n'est pas une valeur possible pour x.

L'algorithme pour résoudre une inéquation est le même que pour résoudre une équation, avec une exception :

Si on multiplie ou divise les deux côtés par une valeur négative, alors on doit changer l'orientation du signe plus ou moins.

Par exemple, supposons qu'on doive résoudre l'inéquation suivante pour x:

On choisit de rassembler les termes contenant l'inconnue à gauche, et les termes ne le contenant pas à droite. On soustrait donc 10x des deux côtés, et on ajoute 12 aux deux côtés, et on simplifie. Cela donne:

Maintenant, on doit se débarrasser du -4, mais comme il multiplie x, on doit le diviser des deux côtés. Cela veut dire qu'on divise les deux côtés par un nombre négatif, et la règle dit que si on fait ça, on doit changer la direction du signe plus ou moins.

On notera qu'on aurait pu éviter cette complication en appliquant une règle alternative : éviter de rassembler les termes contenant x de manière à obtenir un terme négatif.

La solution dit la même chose : x est plus grand que -3,75.