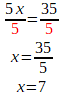Notre algorithme nous évite te toucher à l'inconnue: qu'elle soit à gauche ou à droite n'a aucune importance tant qu'on arrive à l'isoler.

Cependant, il est parfois nécessaire de la déplacer de gauche à droite ou inversement. Par exemple: si elle est coincée dans le dénominateur d'une fraction. On doit alors appliquer les mêmes techniques pour la mettre "en haut".

Rassembler et combiner les termes qui contiennent l'inconnue du même côté du signe égal

Ici, il n'y a qu'un seul terme contenant l'inconnue. Nous pouvons passer à l'étape suivante.

Rassembler et combiner les termes ne contenant pas l'inconnue de l'autre côté du signe égal

Le terme à faire passer de l'autre côté du signe égal est le -3. La seule manière de l'annuler est d'ajouter 3 au côté droit. Pour équilibrer, on fait la même chose au côté gauche.

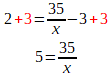
Faire l'inverse de ce qui est fait à l'inconnue aux deux côtés du signe égal

Ici, c'est x qui fait quelque chose: il divise 35. On fait l'inverse de ce qu'il fait: on multiplie les deux côtés par x. Comme à droite, il y a un x dans le numérateur et un x dans le dénominateur, ils s'annulent:

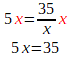
Comme on n'a pas fini, il faut répéter la dernière étape de l'algorithme:

Faire l'inverse de ce qui est fait à l'inconnue aux deux côtés du signe égal

Comme l'inverse de multiplier par cinq est diviser par cinq, on divise les deux côtés par cinq: