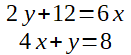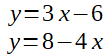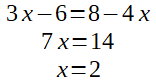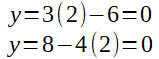On peut se retrouver dans des situations où le problème a non pas une mais deux inconnues. Tant qu'on a autant d'équations que d'inconnues, on peut résoudre le problème. L'algorithme utilisé est le même, avec deux petites modifications.

Rassembler et combiner les termes qui contiennent l'inconnue du même côté du signe égal; rassembler et combiner les termes ne contenant pas l'inconnue de l'autre côté du signe égal.

Ici, on a deux inconnues. Il faut choisir par quelle inconnue on va commencer. Dans les deux équations, y semble le plus simple à gérer (pas de facteur), donc résolvons les deux équations pour y.

ou

Voici maintenant l'étape que nous devons rajouter:

Remplacer l'inconnue dans la deuxième équation par l'expression à laquelle elle correspond dans la première.

Pour mémoire, l'expression, c'est tous les termes à droite du signe égal.

Ensuite, on reprend l'algorithme depuis le début.

Rassembler et combiner les termes qui contiennent l'inconnue du même côté du signe égal; rassembler et combiner les termes ne contenant pas l'inconnue de l'autre côté du signe égal.

On a trouvé une des deux inconnues! Pour trouver l'autre, il faut mettre ce résultat dans l'une des deux équations. Pour vérifier que c'est bien la deuxième solution, j'utilise les deux équations: je remplace x par la valeur que j'ai trouvé.

On a trouvé les deux solutions au système d'équation.