Dans l’exemple suivant, on doit calculer deux quantités. Nous allons appliquer notre procédure pour clarifier ce qu’on doit faire, et vérifier nos résultats par la méthode graphique.
Une voiture est à une position x₀ = 100. A un moment t = 0, elle accélère à 3 m/s². Trouver la position de la voiture après 5 secondes, et calculer le temps qu’elle prendra pour arriver à x = 200 m.
On donne la fonction suivante:
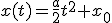
x(t) = \frac{a}{2}t^2 + x_0
On devine du contexte de l’exercice que :
-
x(t) correspond à la position
-
t correspond au temps
-
a correspond à l’accélération : 3 m/s²
-
x₀ correspond à la position initiale (la position de départ) : 100 m
On écrit donc la fonction :
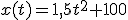
x(t) = 1,5 t^2 + 100
La première question nous demande de trouver une position à un certain temps. Sachant qu’on est parti de t = 0, on a juste à remplacer t par la valeur donnée : 5 s.
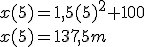
x(5) = 1,5(5)^2 + 100 \\ x(5)= 137,5 m
La deuxième question nous demande de trouver un temps correspondant à une position. On remplace donc x(t) par la valeur donnée : 200 m, et on résout.
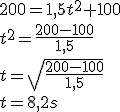
200 = 1,5 t^2 + 100\\ t^2 = \frac{200 - 100}{1,5}\\ t = \sqrt{\frac{200 - 100}{1,5}}\\ t = 8,2 s
On notera au passage que l'inverse d'un carré est une racine carrée.
On peut enfin reporter les résultats de nos calculs : la voiture atteindra la position x = 137,5 m après 5 secondes, et atteindra la position x = 200 m après 8,2 s.
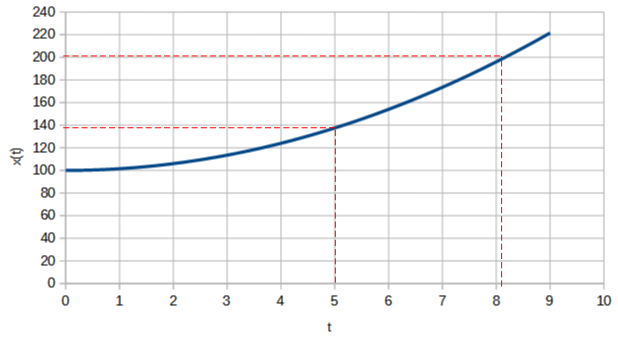 En complétant un tableau de valeurs à l’aide d’une feuille de calcul, on peut confirmer graphiquement nos résultats :
En complétant un tableau de valeurs à l’aide d’une feuille de calcul, on peut confirmer graphiquement nos résultats :
-
L’image de t = 5 est égale à un peu moins de 140
-
L’antécédent de 200 est égal à un peu plus de 8
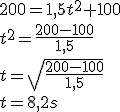
 En complétant un tableau de valeurs à l’aide d’une feuille de calcul, on peut confirmer graphiquement nos résultats :
En complétant un tableau de valeurs à l’aide d’une feuille de calcul, on peut confirmer graphiquement nos résultats :