Trouver une fonction à partir de données
Dans un graphique ou dans un énoncé, il arrive qu’on puisse identifier les coordonnées de deux points. A partir de ces coordonnées, on peut déterminer le coefficient directeur a et l’ordonnée à l’origine b en suivant l’algorithme suivant :
|
Algorithme |
Exemple |
|
Organiser les coordonnées par ordre croissant de x |
(2 ; 13) (4 ; 19) |
|
Calculer le changement en f(x) – le deuxième moins le premier |
19 - 13 = 6 |
|
Calculer le changement en x – le deuxième moins le premier |
4-2 = 2 |
|
Diviser le changement en f(x) par le changement en x. C’est le coefficient directeur a de notre fonction affine. |
a = \frac{\Delta f(x)}{\Delta x}\\ a = \frac{6}{2} = 3 |
|
Dans f(x) = ax + b, remplacer f(x) et x par les coordonnées d'un des deux points, et a par la valeur que vous avez trouvé. Dans l'exemple ci-contre, je le fais avec les deux points, mais vous n'en avez vraiment besoin que d'un. |
f(x) = ax + b\\ 13 = 3(2) + b\\ 19 = 3(4) + b |
|
Résoudre pour b. Dans l'exemple ci-contre, je le fais avec les deux points, mais vous n'en avez vraiment besoin que d'un. |
13 - 3(2) = b\\ b = 7\\ 19-3(4) = b\\ b = 7 |
|
Écrire le résultat. |
f(x) = 3x + 7 |
Une manière plus concise d'écrire cet algorithme est d’utiliser les formules qu’en fait il décrit :
Pour les points :
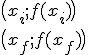
\big(x_i ; f(x_i)\big)\\ \big(x_f ; f(x_f)\big)
Le coefficient directeur a est le ratio du changement en f(x) sur le changement en x.
![]()
a = \frac{f(x_f)-f(x_i)}{x_f - x_i}
L'ordonnée à l'origine est obtenue en insérant les coordonnées d'un des deux points dans la fonction linéaire, et de résoudre cette équation pour b.
![]()
f(x_i) = a (x_i) + b\\ b = f(x_i) - a(x_i)
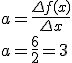
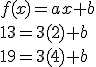
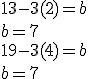
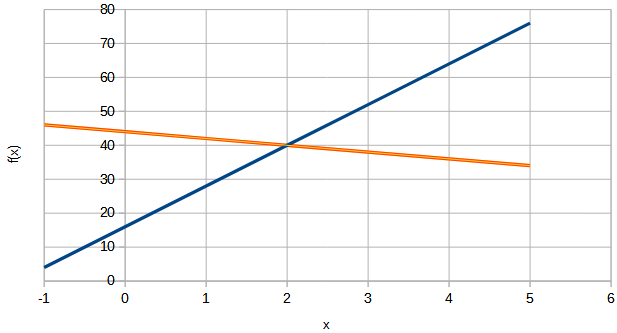 Au début
Au début 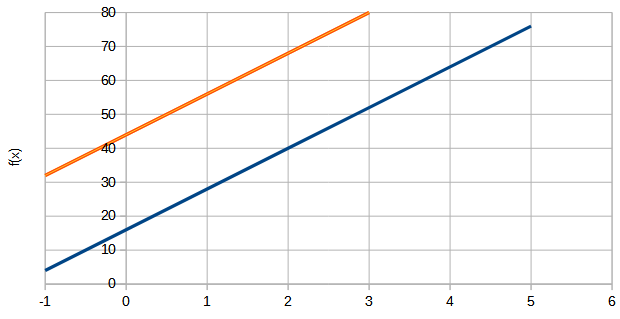 Il existe un cas où résoudre un système d’équations est impossible : lorsque les deux fonctions qui leur correspondent ont le même coefficient directeur
Il existe un cas où résoudre un système d’équations est impossible : lorsque les deux fonctions qui leur correspondent ont le même coefficient directeur