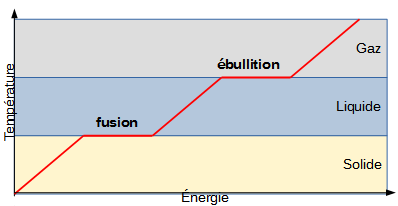
 Si on mesure l'évolution de la température au cours du temps lorsqu'on chauffe un matériau, on observe un phénomène à première vue étrange: la température cesse d'augmenter après un certain temps. Le moment où ce phénomène se produit correspond au moment où le matériau change de phase (solide à liquide, liquide à gaz, etc.).
Si on mesure l'évolution de la température au cours du temps lorsqu'on chauffe un matériau, on observe un phénomène à première vue étrange: la température cesse d'augmenter après un certain temps. Le moment où ce phénomène se produit correspond au moment où le matériau change de phase (solide à liquide, liquide à gaz, etc.).
Ce phénomène est en fait tout à fait normal: il faut de l'énergie pour changer la phase d'un matériau. Arrivé au point de fusion ou d'ébullition, toute l'énergie donnée au matériau ne contribue plus à une augmentation de température mais à un changement de phase. On peut alors dire que de l'énergie est stockée dans la phase d'un matériau.
L'enthalpie de changement de phase ΔH est la quantité d'énergie requise pour changer la phase d'une quantité d'un matériau. Par exemple, l'enthalpie de fusion (phase solide à phase liquide) de l'eau et de 333.55 kJ kg-1. Cela signifie que pour faire fondre un kilogramme de glace, il faut 333,55 kilojoules d'énergie.
On peut utiliser la définition de l'enthalpie pour écrire une nouvelle formule permettant de calculer l'énergie émise ou reçue par un changement de phase:
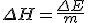
\Delta H = \frac{\Delta E}{m}
Résolvant cette expression pour ΔE:
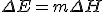
\Delta E = m \Delta H
Si le matériau passe d'une phase à une phase supérieure (solide à liquide ou liquide à gaz), de l'énergie lui est donnée: cette énergie est positive.
Si le matériau passe d'une phase à une phase inférieure, le matériau perd de l'énergie et la restitue à son environnement: cette énergie est négative.
![]()
![]()
 Si on mesure l'évolution de la température au cours du temps lorsqu'on chauffe un matériau, on observe un phénomène à première vue étrange: la température cesse d'augmenter après un certain temps. Le moment où ce phénomène se produit correspond au moment où le matériau change de phase (solide à liquide, liquide à gaz, etc.).
Si on mesure l'évolution de la température au cours du temps lorsqu'on chauffe un matériau, on observe un phénomène à première vue étrange: la température cesse d'augmenter après un certain temps. Le moment où ce phénomène se produit correspond au moment où le matériau change de phase (solide à liquide, liquide à gaz, etc.).