Forces en rotation
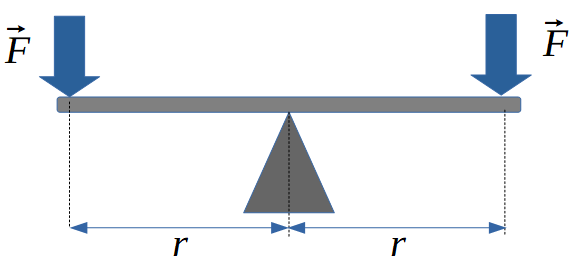 Supposons une masse posée au bout d'une flèche. La flèche est libre de tourner autour d'un axe.
Supposons une masse posée au bout d'une flèche. La flèche est libre de tourner autour d'un axe.
La masse subit la gravité. Elle pousse donc sur le bout de la flèche avec une force Fg. Pour que la flèche ne tourne pas autour du point d'appui, il faudrait mettre une masse égale à la première masse à une distance égale du point d'appui, mais de l'autre côté. Ainsi, la même force Fg est appliquée aux deux bouts. C'est le principe de la balance.
Maintenant, supposons que les bouts de flèches ne soient pas à la même distance du point d'appui. Il faudrait alors changer les masses pour que le système reste en équilibre. 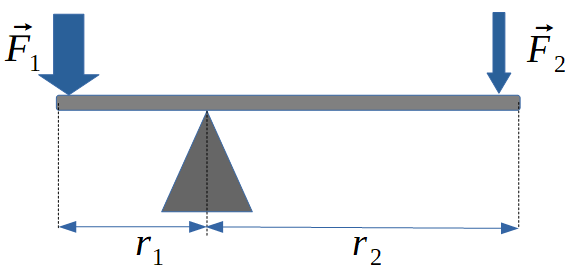 On a vu que dans le premier cas, les forces F et les distances r étaient égales. Ici, les distances r sont différentes. En toute logique, les forces F devraient elles aussi être différentes.
On a vu que dans le premier cas, les forces F et les distances r étaient égales. Ici, les distances r sont différentes. En toute logique, les forces F devraient elles aussi être différentes.
Un moment M est une force appliquée par rapport à un axe de rotation. Il est défini comme étant le produit de la force avec la distance entre le point d'application de la force et l'axe de rotation.
![]()
M = F r
Un moment qui ferait tourner le système (ici, la flèche et la masse) dans le sens inverse des aiguilles d'une montre est positif; dans le sens des aiguilles d'une montre, il est négatif.
La première loi de Newton s'applique aux moments. Ici, cette loi dit donc que la somme des moments dans un système statique (qui n'accélère pas) est égale à zéro.
![]()
\sum{M} = 0
Dans notre balancier, il y a deux forces: F1 et F2. Il y a donc deux moments: M1 pousse la flèche dans le sens inverse des aiguilles d'une montre, et M2 pousse dans le sens des aiguilles d'une montre: le premier est donc positif, le second négatif.
![]()
M_1 = F_1 r_1 \\ M_2 = -F_2 r_2
En appliquant la première loi de Newton et en résolvant pour F2 , on obtient la loi du levier:
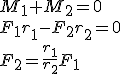
M_1 + M_2 = 0 \\ F_1 r_1 - F_2 r_2 = 0 \\ F_2 = \frac{r_1}{r_2} F_1
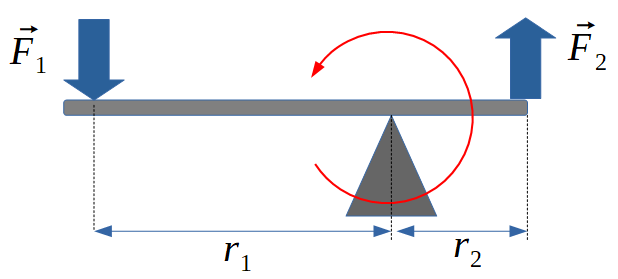
Si r1 est supérieur à r2, alors le ratio devant F1 est plus grand que un: F2 est plus grand que F1. Si r1 est inférieur à r2, alors le ratio devant F1 est plus petit que un: F2 est plus petit que F1.
Intuitivement, on sait que les moments doivent être égaux: c'est le principe d'Archimède - le levier. Si on pousse avec une certaine force sur le bout long d'un levier, on retrouve une force multipliée au bout cours du levier. Le coefficient multiplicateur est donné par le ratio des distances entre points d'application des forces et point d'appui du levier.
Un couple C est la somme d'une paire de moments qui vont dans la même direction: dans le sens des aiguilles d'une montre, ou dans le sens inverse.
![]()
C = F d
Il faut noter qu'en ingénierie, on a tendance à confondre couple et moment. Si leur définitions sont différentes, leur valeurs numériques sont égales. On retrouve l'idée du couple dans les clefs à couple qui permettent de limiter la force avec laquelle on sert un boulon.
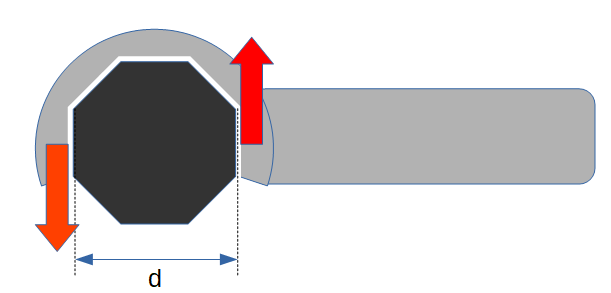
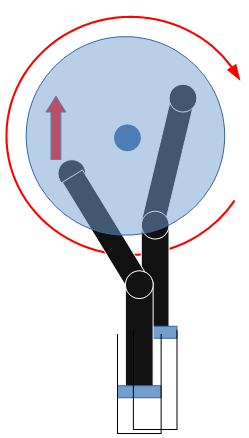 Le terme "couple" est un peu un abus de langage; on parle réellement de moment. Lors d'une explosion, un piston pousse un arbre connecté à un volant: il applique donc une force à une certaine distance d'un axe de rotation, ce qu'on appelle en physique un moment. Puis, un autre piston pousse sur le même volant, forçant le premier piston à revenir à sa position initiale.
Le terme "couple" est un peu un abus de langage; on parle réellement de moment. Lors d'une explosion, un piston pousse un arbre connecté à un volant: il applique donc une force à une certaine distance d'un axe de rotation, ce qu'on appelle en physique un moment. Puis, un autre piston pousse sur le même volant, forçant le premier piston à revenir à sa position initiale.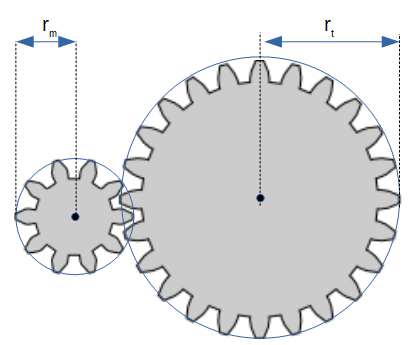 On peut donc réécrire:
On peut donc réécrire: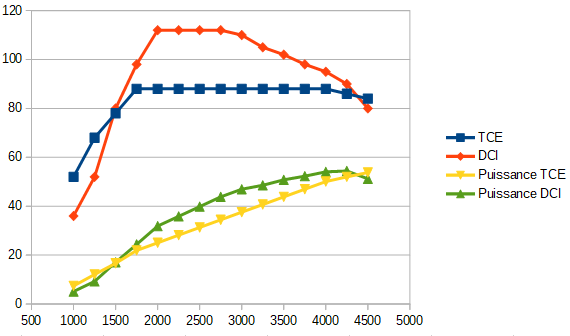 Par exemple, le graphique compare le rapport entre puissance et couple pour deux moteurs (un essence, un diesel) à différents régimes (tours par minute). On peut remarquer que si les moteurs montent en puissance régulièrement, le moteur diesel a plus de couple à bas régime que le moteur essence. On peut aussi déterminer le nombre de tours par minute auquel un changement de vitesse est recommandé: lorsqu'on arrive à un plateau pour le couple, augmenter le régime ne fait qu'augmenter la consommation. Pour les deux moteurs, on devrait passer à la vitesse supérieure aux alentours de 2000 tours sur terrain plat.
Par exemple, le graphique compare le rapport entre puissance et couple pour deux moteurs (un essence, un diesel) à différents régimes (tours par minute). On peut remarquer que si les moteurs montent en puissance régulièrement, le moteur diesel a plus de couple à bas régime que le moteur essence. On peut aussi déterminer le nombre de tours par minute auquel un changement de vitesse est recommandé: lorsqu'on arrive à un plateau pour le couple, augmenter le régime ne fait qu'augmenter la consommation. Pour les deux moteurs, on devrait passer à la vitesse supérieure aux alentours de 2000 tours sur terrain plat.