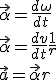Mouvement
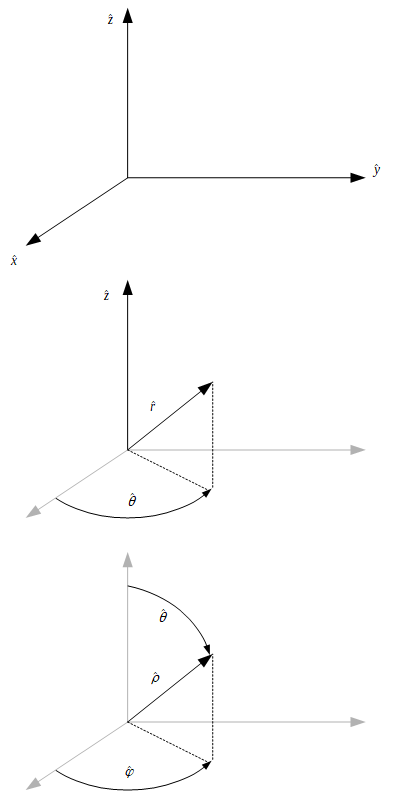Dans un premier temps, nous définissons un déplacement Δx. A ce stade, rappelez-vous que nous choisirons la lettre x pour simplifier, mais toutes les lois de la mécanique s'appliquent de même dans toutes les dimensions : cartésiennes (x, y et z), cylindriques (θ, r et z) et sphériques (θ, ρ et φ).
Un mouvement est simplement un déplacement effectué sur un temps Δt. Il y a beaucoup de types de mouvements, mais on se limitera à deux: la vitesse v et l'accélération a.
Avant d'aller plus loin dans dans cette révision de concepts vus au collège et au lycée, quelques précisions sur la notation à partir d'ici :
- Nous allons aussi devoir utiliser des variations Δ plus petites (infiniment petites, en fait) pour pouvoir aller de fonction en fonction. Nous écrirons alors nos variations avec un d (pour dérivée). A ce stade, si vos dérivées et vos primitives sont un peu rouillées, je vous invite à considérer ce cours sur les fonctions.
- Nous allons indiquer si la quantité a une direction (symbolisée par un accent circonflexe) en plus d'une norme, bref, si c'est un vecteur.
\vec{x} = x \hat{r}
- Par soucis de clarté (et de facilité dans le codage des formules), lorsqu'un vecteur sera une dérivée, j'ignorerai la flèche, ne précisant la direction que lorsqu'elle a un rôle particulier (je pense aux produits vectoriels).
Ces précisions étant faites, définissons nos deux mouvements : la vitesse v et l'accélération a.
\vec{v}=\frac{dx}{dt}\\\vec{a}=\frac{dv}{dt}
A partir de ces deux définitions, nous pouvons créer une fonction qui décrit la vitesse et la position d'un particule en fonction du temps.
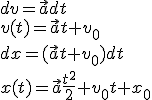
dv = \vec{a} dt\\ v(t) = \vec{a} t + v_0\\ dx= (\vec{a} t + v_0)dt\\ x(t)= \vec{a} \frac{t^2}{2} + v_0 t + x_0
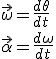
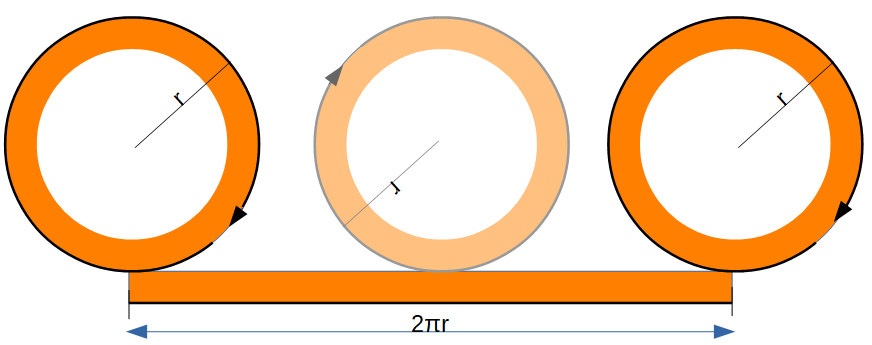Considérons maintenant ceci : si le déplacement total d'une roue dans le sens de θ est un tour complet, alors la distance linéaire est égale au périmètre de la roue. Si, au lieu de faire un tour complet, elle ne parcours qu'un angle dθ, alors:
