L'énergie et le temps
La puissance est une quantité qui estime la quantité de travail que l'on peut faire en un certain temps. Comme le travail, c'est de l'énergie :
![]()
P = \frac{dE}{dt}
L'unité de puissance est le joule seconde J.s ou, plus communément, le watt W.
Comme l'énergie, la puissance est une de ses quantités qui permettent d'appliquer directement le principe de conservation de l'énergie. Nous allons donc revisiter certains concepts avec la puissance.
Par exemple, reprenons l'énergie potentielle. Nous savons que le travail pour soulever quelque chose à vitesse constante est le produit de la force due à la gravité avec la distance verticale parcourue. Si nous prenons la dérivée par rapport au temps:
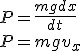
P = \frac{mg dx}{dt}\\ P = mg v_x
On peut donc calculer la puissance effective d'une machine en multipliant la force due à la gravité agissant sur elle par la vitesse à laquelle elle grimpe.
Qu'en est-il d'une masse qui accélère (par exemple, une voiture) ? Hé bien le travail est le produit de la force appliquée (masse fois accélération) multiplié par la distance parcourue pendant cette accélération. Si on connaît la distance parcourue :
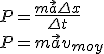
P = \frac{m \vec{a} \Delta x}{\Delta t}\\ P = m \vec{a} v_{moy}
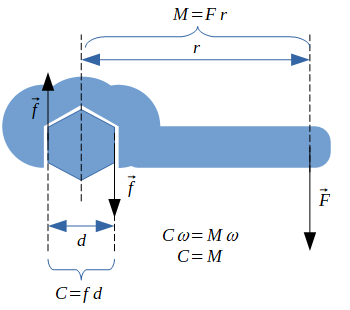 Un troisième exemple est le moment - ou ce que certains ingénieurs appellent, par abus de langage, le couple C. Si ce n'a pas la même définition stricte (le couple est un couple de moments qui vont dans la même direction), les deux réfèrent à la même quantité (voir l'illustration ci-contre). Parlant de puissance, nous parlerons donc de couple.
Un troisième exemple est le moment - ou ce que certains ingénieurs appellent, par abus de langage, le couple C. Si ce n'a pas la même définition stricte (le couple est un couple de moments qui vont dans la même direction), les deux réfèrent à la même quantité (voir l'illustration ci-contre). Parlant de puissance, nous parlerons donc de couple.
Le travail fait par un couple est toujours sur une distance mais cette fois, la distance est un angle. Oui, il faut se rappeler que le couple est une force appliquée autour d'un axe de rotation.
![]()
dW = C d\theta
Comme avant, je divise le tout par le temps. On trouve alors une formule pour trouver la puissance à partir du couple et de la vitesse angulaire.
![]()
P = C \frac{d\theta}{dt}\\ P = C \omega