Variations d'une fonction
La dérivée est une fonction représentant la variation d’une autre fonction. On a vu quelque chose de similaire en physique : le changement d’une variable, comme la position, sur le changement d’une autre variable, comme le temps.
![]()
v(t) = \frac{\Delta x}{\Delta t}
La dérivée d’une fonction f(x), notée f’(x), est la variation de la fonction f(x) sur x.
Si la fonction est constante -ne dépend pas de x - par définition il n’y a pas de variation.
![]()
f(x) = c
La dérivée d’une constante est donc égale à zéro.
![]()
f'(x) = 0
Pour une fonction linéaire, la variation est donnée par le coefficient directeur :
![]()
a = \frac{f(x_2)-f(x_1)}{x_2 - x_1}
La dérivée d'une fonction linéaire est donc simplement une constante : son coefficient directeur.
![]()
f(x) = a x
![]()
f'(x) = a
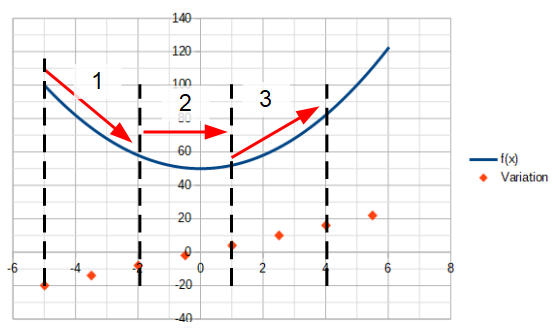 Pour une fonction carrée ( de degré 2), ça semble un peu plus compliqué. En effet, la variation en chaque point d’une parabole semble changer en permanence.
Pour une fonction carrée ( de degré 2), ça semble un peu plus compliqué. En effet, la variation en chaque point d’une parabole semble changer en permanence.
En 1, la courbe descend, donc la variation est négative. En 2, la courbe ne varie quasiment pas, donc la variation est égale à 0. En 3, la courbe remonte, donc la variation est positive.
On note toutefois que les points représentant la variation dans différentes intervalles sur x forment une fonction linéaire (ou affine). Plus on réduit l'espace entre x2 et x1, plus on obtient de points formant la ligne. En d'autres termes, plus Δx approche de zéro, plus la fonction dérivée est complète. En calculant simplement le coefficient directeur de la ligne formée par ces points, on obtient l'équation de ligne de la dérivée.
Ci-dessous, j’ai calculé le coefficient directeur de cette fonction affine pour plusieurs fonctions carrés différentes.
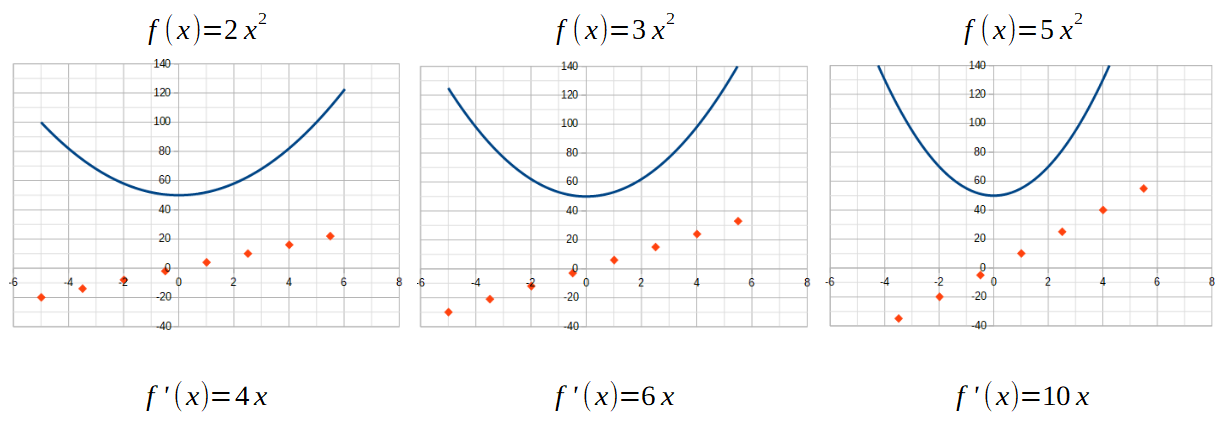
On note que le coefficient directeur de la fonction affine représentant la variation de la fonction carré est toujours le double du coefficient directeur de cette dernière.
![]()
f(x)= a x^2
La dérivée d'une fonction carré est donc:
![]()
f'(x)= 2 a x
En observant les résultats qu’on a obtenu, on peut discerner un motif : la dérivé d’une fonction est une fonction dont le coefficient directeur est multiplié par le degré, et de degré inférieur à la première fonction. On peut donc écrire une formule pour f'(x) en fonction d'une fonction simple f(x).
![]()
f(x) = a x^n
![]()
f'(x) = na x^{n-1}
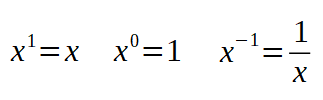 Avant d'étudier un exemple avec un polynôme du second degré, rappelez-vous des quelques propriétés des puissances ci-contre.
Avant d'étudier un exemple avec un polynôme du second degré, rappelez-vous des quelques propriétés des puissances ci-contre.
Un polynôme du second degré est la somme de trois fonctions dont nous venons de voir les dérivées: une carré, une linéaire, et une constante.
![]()
f(x) = 2 x^2 + 4 x + 10
La dérivée de la première fonction est, appliquant la formule que nous avons trouvé:
![]()
2 x^2 \Longrightarrow (2\times 2)x^{2-1} \Longrightarrow 4 x
Appliquant la même formule à la deuxième fonction:
![]()
4 x \Longrightarrow (4 \times 1)x^{1-1} \Longrightarrow 4 x^0 \Longrightarrow 4
La dernière partie est une constante, dont nous avons vu que la dérivée est égale à zéro. On peut même le prouver:
![]()
10 \Longrightarrow 10 x^0 \Longrightarrow (10 \times 0)x^{0-1} \Longrightarrow 0 x^{-1} \Longrightarrow \frac{0}{x} = 0
On regroupe tous ces résultats dans la dérivée de notre polynôme du second degré:
![]()
f'(x) = 4 x + 4