Dans un premier temps, nous allons voir des fonctions qui ressemblent à ça :

Une fonction "prête à l'emploi" contient des valeurs pour trois nombre: le coefficient directeur a, l'ordonnée à l'origine b et l'exposant ou degré n. Pour obtenir l'image du nombre x, on remplace le x par un nombre, et on fait le calcul.

Dans les descriptions suivantes, j'ai ajouté des animations décrivant le comportement d'une fonction lorsque son coefficient directeur a passe de négatif à positif. Tentez d'identifier les coefficients a et b dans les formules indiquées sur les animations, et observez le comportement de la courbe quand on change a.

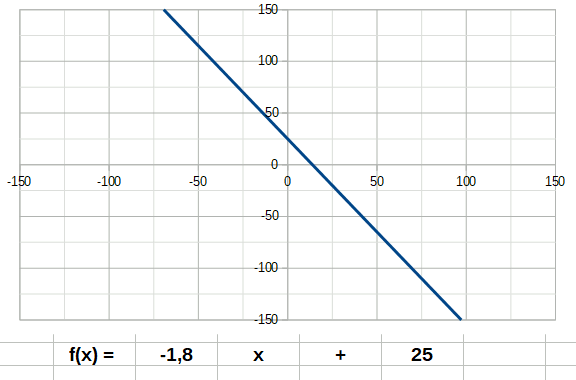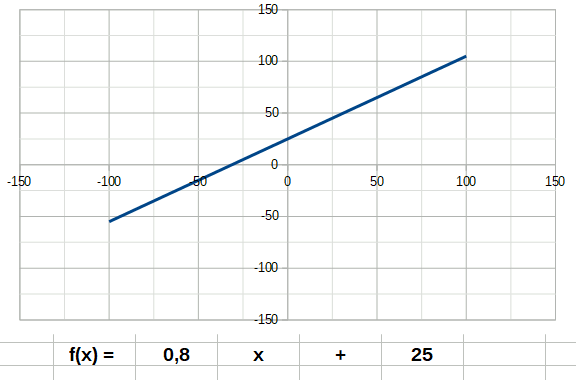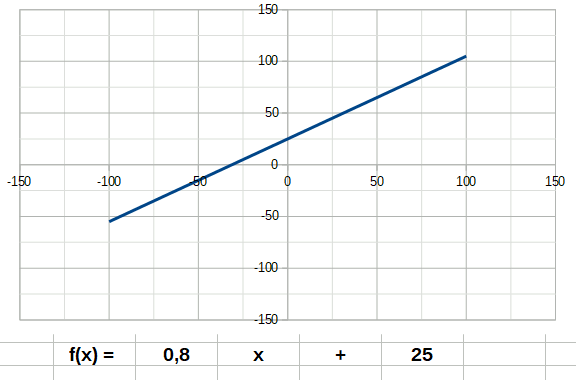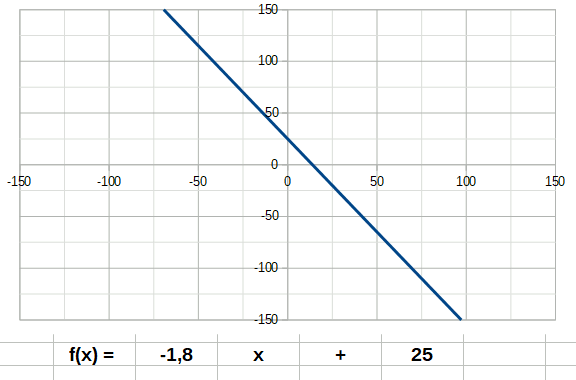Un premier exemple de fonction est la fonction affine ou linéaire. Son degré n est égal à 1. Elle a donc la forme:

Une fonction affine produit, lorsqu'on calcule un grand nombre d'images, une ligne droite.

On remarquera que lorsque a est positif, la fonction augmente à mesure que x → ∞. Si a est négatif, la fonction décroît.

L'ordonnée à l'origine b est la valeur de f(0), c'est à dire l'image de la fonction lorsque x = 0. Si b = 0 : on dit que la fonction est proportionnelle.

Les fonctions de degré 2 et 3 augmentent ou décroissent rapidement.

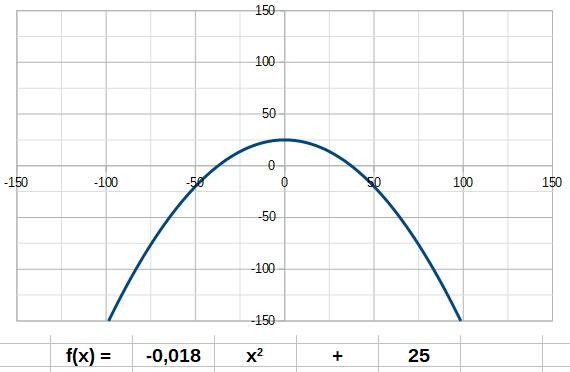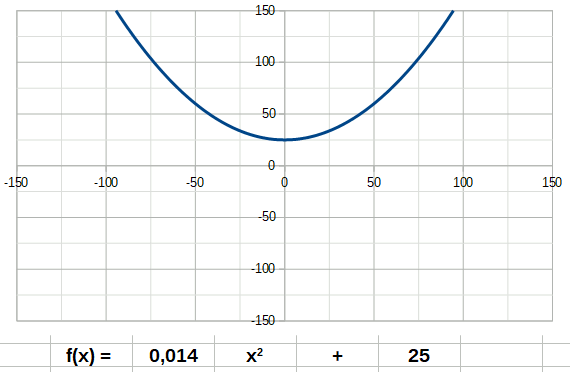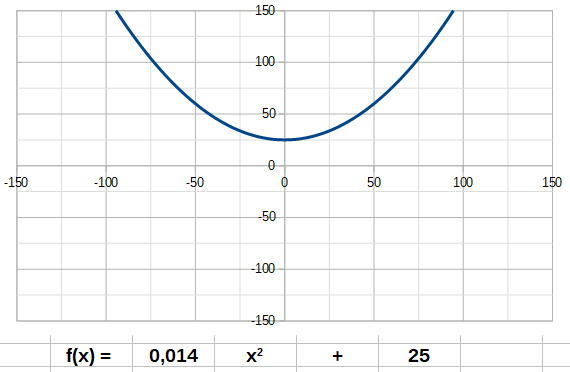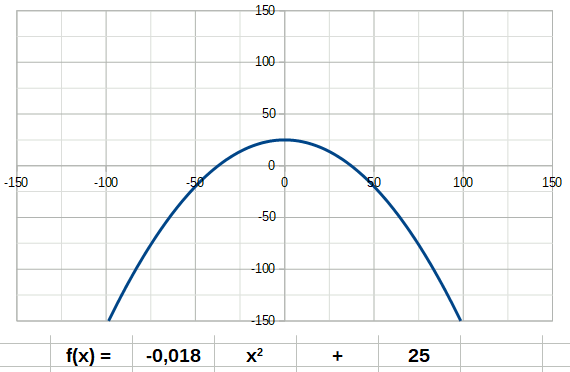La fonction carré (de degré 2) à la forme suivante:

Comme pour la fonction linéaire, b est l'ordonnée à l'origine - l'endroit où la courbe formée par la fonction croise l'axe des ordonnées. Dans l'exemple ci-contre, b = 25.

Si le coefficient directeur est positif, la fonction augmente à mesure que x → ± ∞. Si il est négatif, elle décroît à mesure que x → ± ∞.

La fonction de degré 3 ("cube") se comporte différemment. En effet, si le carré d'un nombre négatif est un nombre positif, il n'en va pas de même pour le cube.

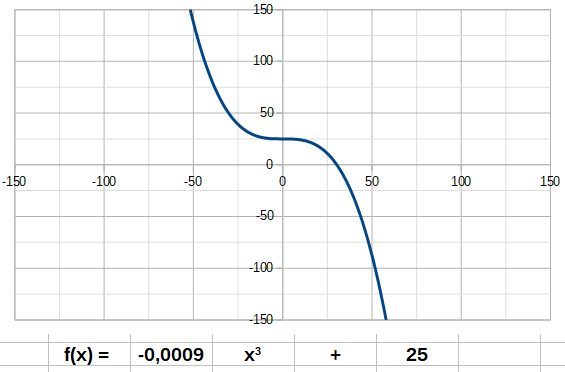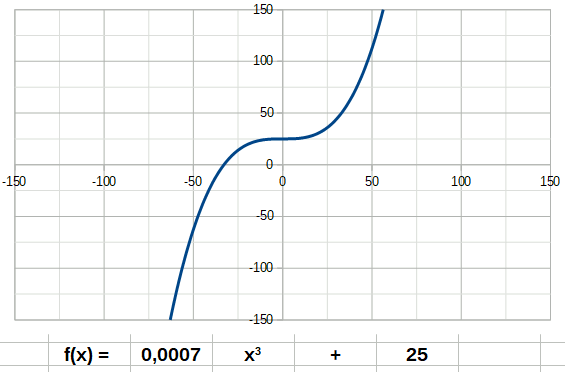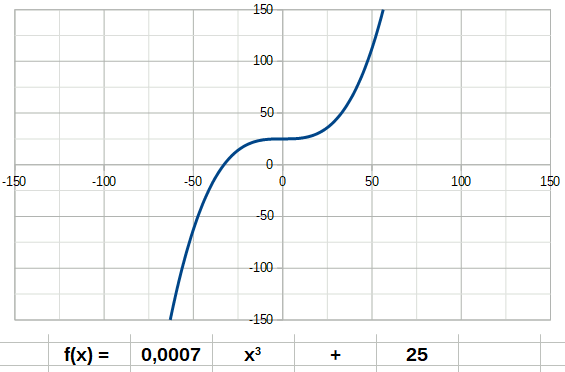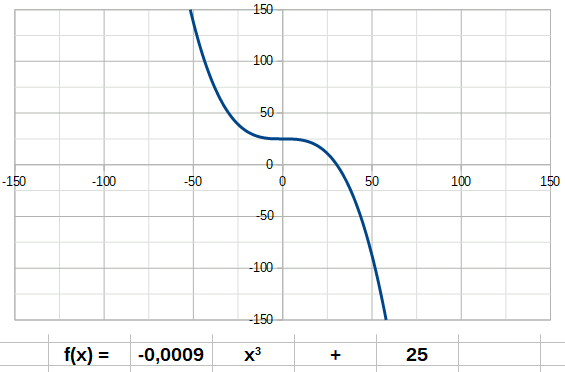La fonction cube a la forme suivante:

Comme toujours, b est l'ordonnée à l'origine.

Lorsque le coefficient a est positif, la fonction décroît lorsque x→-∞ et croît lorsque x→∞. Si a est négatif, la fonction croît lorsque x→-∞ et décroît lorsque x→∞

Une fonction inverse décrit une situation où la variable est inversement proportionnelle à l'image: plus la variable est grande, plus l'image est petite; plus la variable est petite, plus l'image est grande.

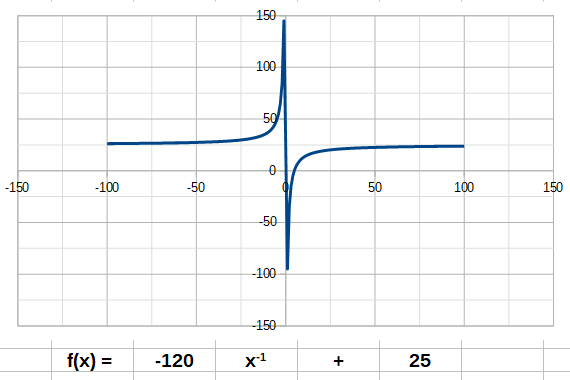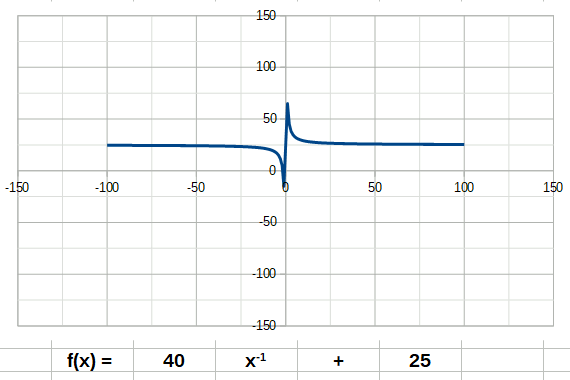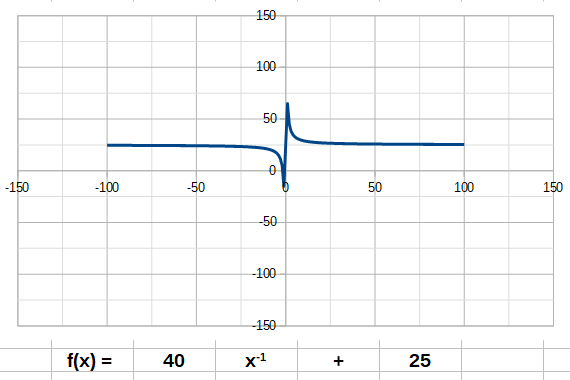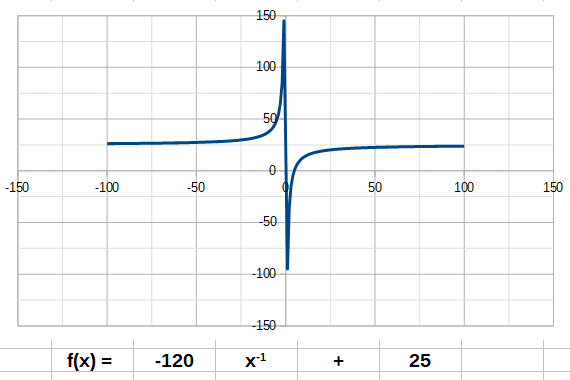La fonction inverse a la forme suivante:

Comme 1/x = x^-1, on peut aussi l'écrire comme suit:

On notera que les choses sont un peu différentes ici. Tout d'abord, b ne correspond plus à l'ordonnée à l'origine. En effet, lorsque x approche de zéro, la fonction approche l'infini. Dans une fonction inverse, b est la valeur vers laquelle f(x) tend à mesure que x croît, que ce soit vers ∞ ou vers -∞. Dans ce cas, on appelle b l'asymptote de la courbe.

Si a est positif, f(x) tend vers -∞ en approchant de zéro par la gauche, et vers ∞ en approchant de zéro par la droite. Si a est négatif, f(x) tend vers ∞ en approchant de zéro par la gauche, et vers -∞ en approchant de zéro par la droite.

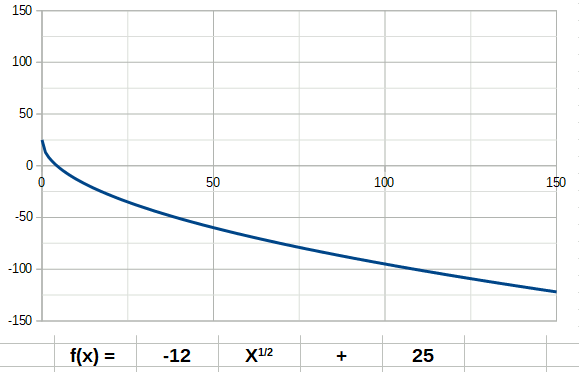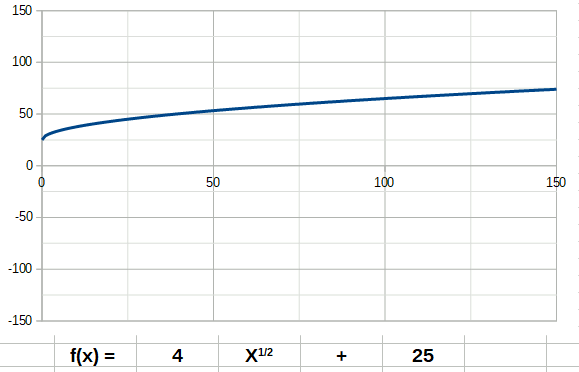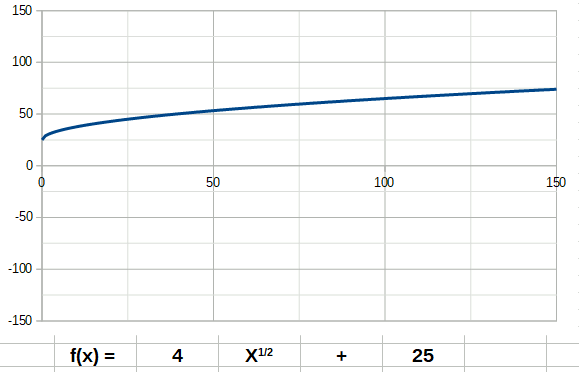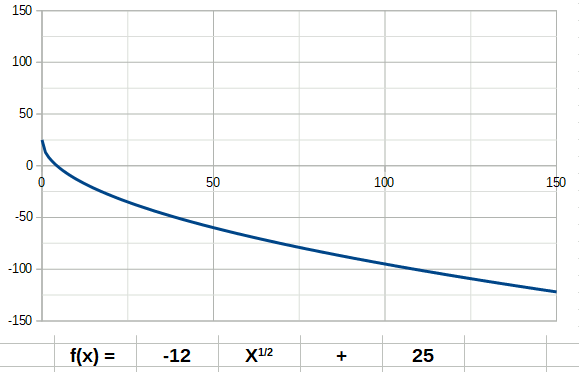La fonction racine a la forme suivante:

Comme une racine carré est égale à l'exposant 1/2, on peut aussi écrire:

On notera qu'à nouveau b est l'ordonnée à l'origine.

Parce que la variable est sous une racine carrée, cette fonction ne donne pas de valeurs réelles pour toute valeur négative.

Si a est positif, f(x) croît; si a est négatif, f(x) décroît.