Définition
Un polynôme du second degré est la somme de deux fonctions : une du premier degré et une du second degré. Leurs constantes b s'additionnent pour former une nouvelle constante: c.
![]()
f(x) = a x^2 + b x + c
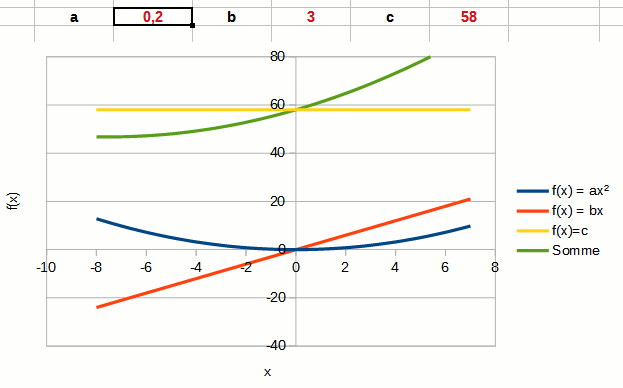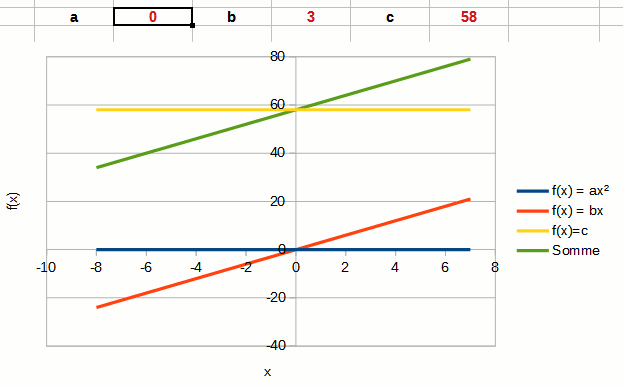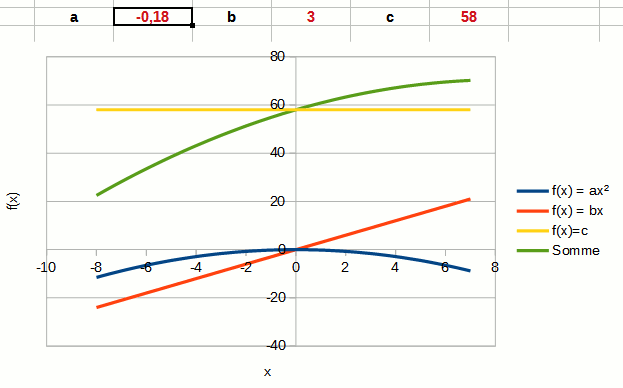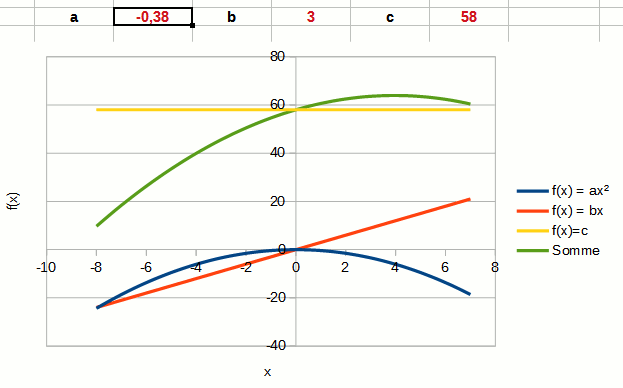 Le coefficient directeur a détermine la forme de la courbe représentant une fonction du second degré.
Le coefficient directeur a détermine la forme de la courbe représentant une fonction du second degré.
Si a est positif, la courbe (qu'on appelle parabole) est ouverte vers le haut. La fonction f(x) est positive quand x → ± ∞. Si a est négatif, la courbe est ouverte vers le bas. La fonction f(x) est négative quand x → ± ∞.
L'animation ci-contre montre le changement de comportement de la fonction quand a change de valeur. La courbe bleue correspond à la fonction carré seule, la courbe verte au polynôme.
Pour tout point de coordonnées (xi ; f(xi)) appartenant à la courbe f(x) :
![]()
a = \frac{f(x_i) - b x_i -c}{x_i^2}
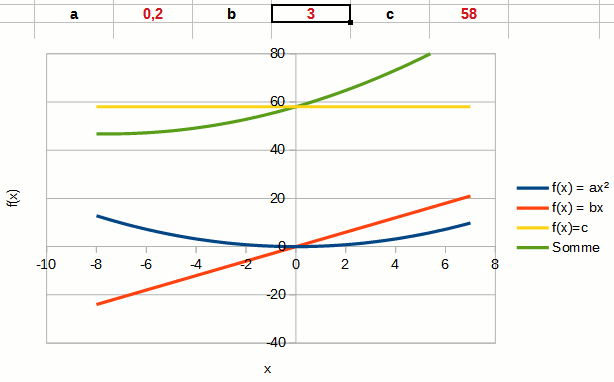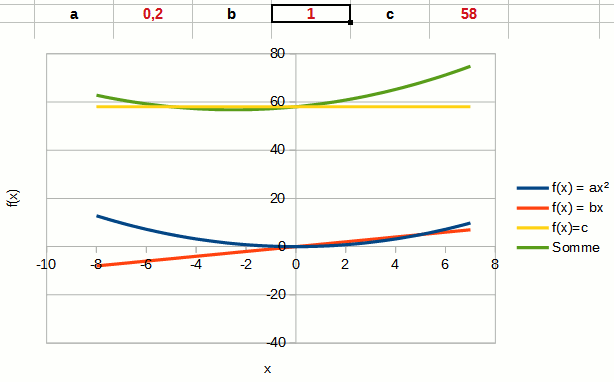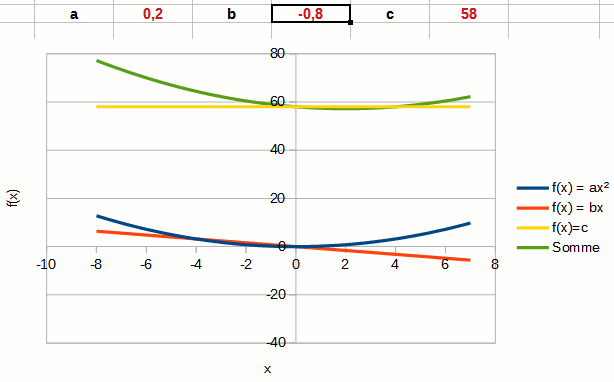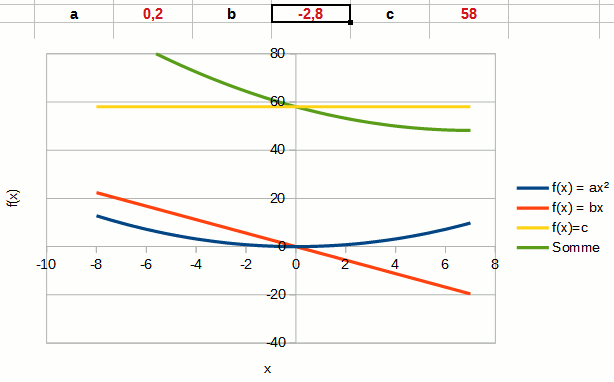 Le coefficient b n'est plus ici l'ordonnée à l'origine, mais le coefficient directeur de la partie linéaire du polynôme.
Le coefficient b n'est plus ici l'ordonnée à l'origine, mais le coefficient directeur de la partie linéaire du polynôme.
On notera que changer b change la position du vertex du polynôme. Le vertex est représenté par les coordonnées du point maximal ou minimal de la parabole.
Plus b est positif, plus le vertex est repoussé vers la gauche. Plus b est négatif, plus le vertex est repoussé vers la droite.
Pour tout point de coordonnées (xi ; f(xi)) appartenant à la courbe f(x) :
![]()
b = \frac{f(x_i) - a x_i^2- c}{x_i}
Dans l'animation, la partie linéaire du polynôme est représentée par la courbe rouge.
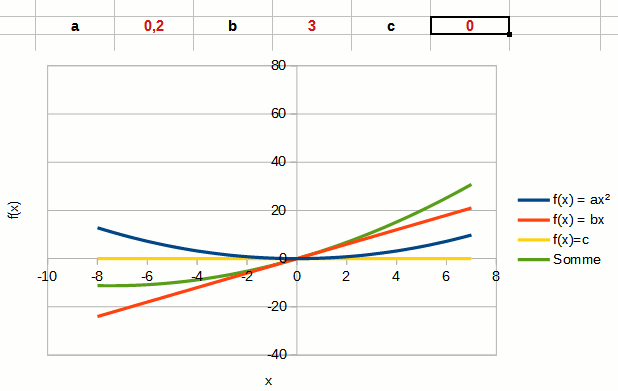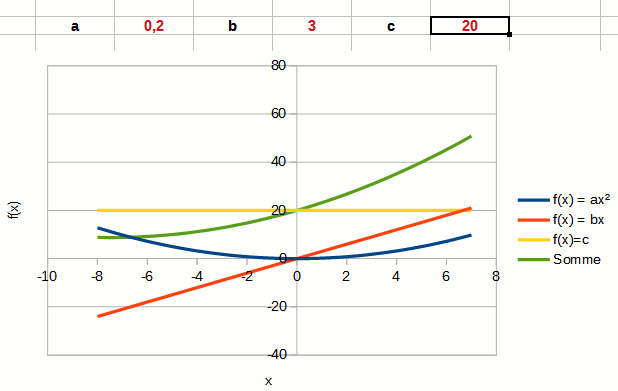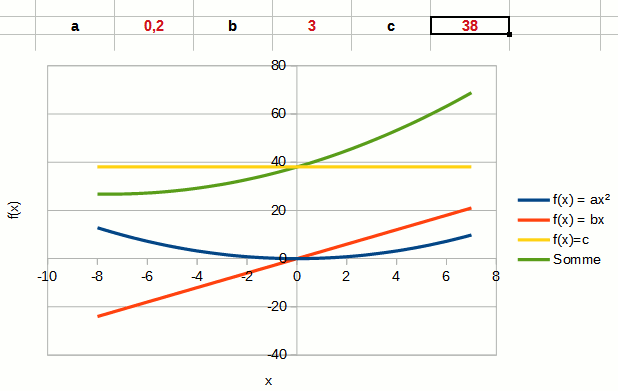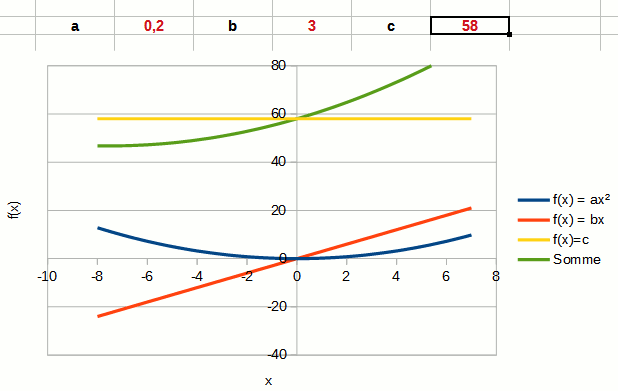 La dernière constante c correspond à une constante, une valeur qui ne change pas quel que soit la valeur de x.
La dernière constante c correspond à une constante, une valeur qui ne change pas quel que soit la valeur de x.
On voit clairement dans l'animation que c , représenté par la courbe jaune, correspond à l'ordonnée à l'origine du polynôme du second degré.
Pour tout point de coordonnées (xi ; f(xi)) appartenant à la courbe f(x) :
![]()
c = f(0)